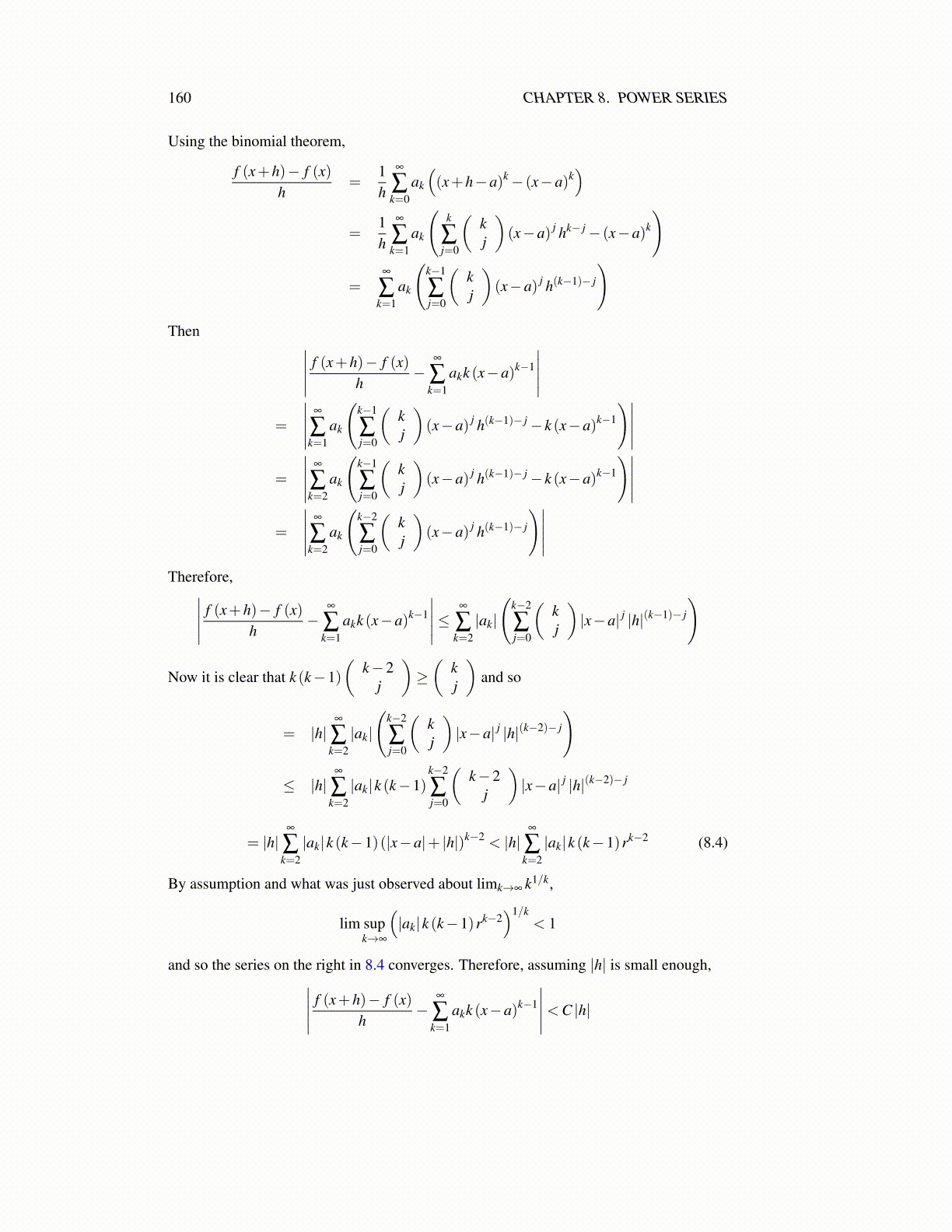
160 CHAPTER 8. POWER SERIES

The above theorem shows that a power series is infinitely differentiable. Does it gothe other way? That is, if the function has infinitely many continuous derivatives, is itcorrectly represented as a power series? The answer is no. See Problem 6 on Page 176for an example. In fact, this is an important example and distinction. The modern theoryof partial differential equations is built on just such functions which have many derivativesbut no correct power series.

8.3 The Special Functions of Elementary CalculusWith this material on power series, it becomes possible to give an understandable treatmentof the exponential function exp and the circular functions, sin and cos. A definition couldbe given directly for x ∈ C but in this section, it is assumed x ∈ R.

8.3.1 Sines and CosinesTo begin with here is a definition of sin,cos, and exp.

Definition 8.3.1 Define for all x ∈ R

sin(x)≡∞

∑k=0

(−1)k x2k+1

(2k+1)!, cos(x)≡

∞

∑k=0

(−1)k x2k

(2k)!,exp(x)≡

∞

∑k=0

xk

k!.

Observation 8.3.2 The above series converge for all x ∈ F. This is most easily seenusing the ratio test. Consider the series for sin(x) first. By the ratio test the series convergeswhenever

limk→∞

|x|2k+3

(2k+3)!

|x|2k+1

(2k+1)!

= limk→∞

1(2k+3)(2k+1)

|x|2

is less than 1. However, this limit equals 0 for any x and so the series converges for allx. The verification of convergence for the other two series is left for you to do and is noharder. In what follows, I will emphasize x real. To do it for arbitrary x ∈ C is really atopic for complex analysis but you use the same series to define these functions.

Now that sin(x) and cos(x) have been defined, the properties of these functions mustbe considered. First, here is a fundamental lemma.

Lemma 8.3.3 Suppose y is an R valued differentiable function and it solves the initialvalue problem,y′′+ y = 0, y(0) = 0,y′ (0) = 0. Then y(x) = 0.

Proof: Multiply the equation by y′ and use the chain rule to write

ddt

(12(y′)2

+12

y2)= 0.

Then by Corollary 7.8.5 12 (y′)2+ 1

2 y2 equals a constant. From the initial conditions, y(0) =y′ (0) = 0, the constant can only be 0.

Theorem 8.3.4 sin′ (x) = cos(x) and cos′ (x) =−sin(x) . Also cos(0) = 1, sin(0) =0 and

cos2 (x)+ sin2 (x) = 1 (8.7)