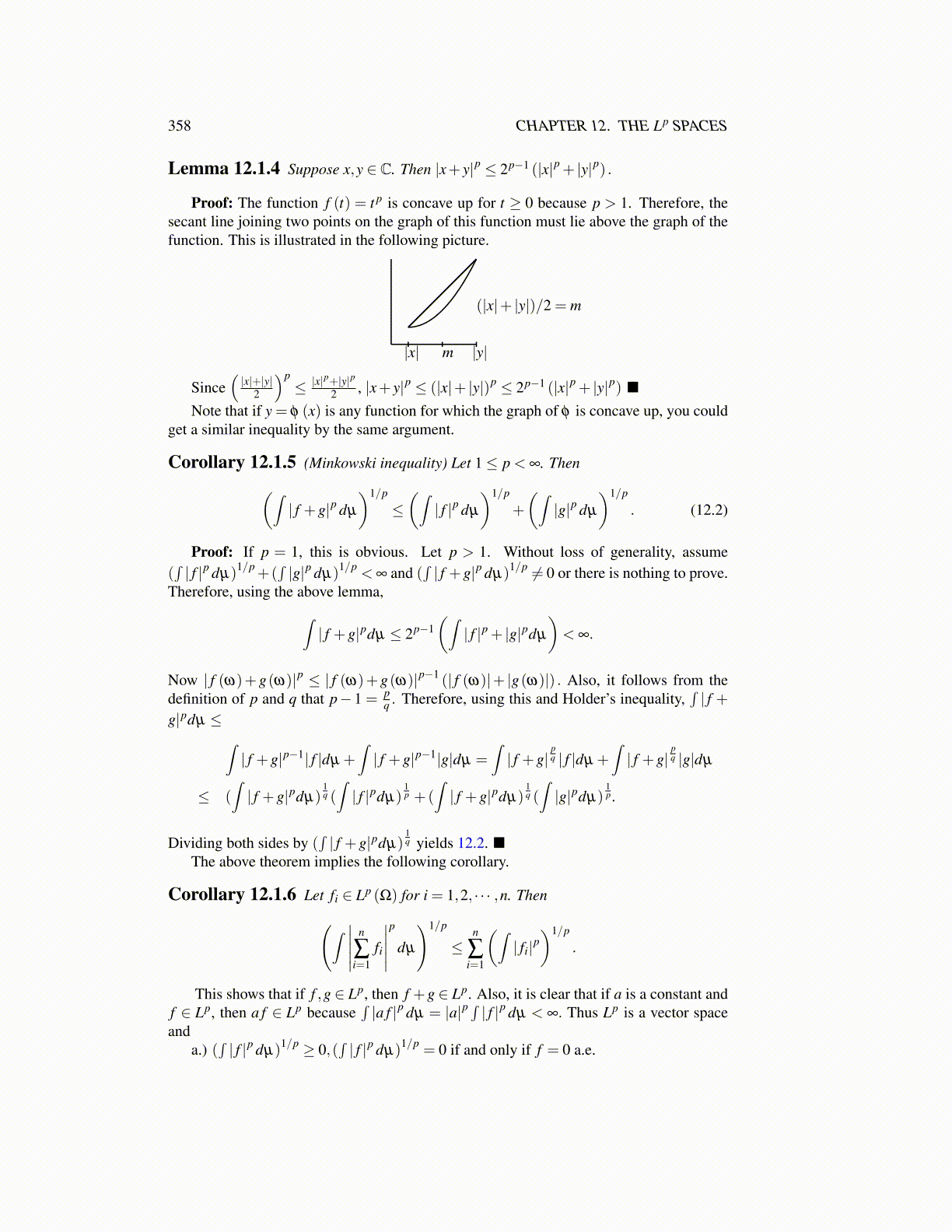
358 CHAPTER 12. THE Lp SPACES

Lemma 12.1.4 Suppose x,y ∈ C. Then |x+ y|p ≤ 2p−1 (|x|p + |y|p) .

Proof: The function f (t) = t p is concave up for t ≥ 0 because p > 1. Therefore, thesecant line joining two points on the graph of this function must lie above the graph of thefunction. This is illustrated in the following picture.

|x| |y|m

(|x|+ |y|)/2 = m

Since(|x|+|y|

2

)p≤ |x|

p+|y|p2 , |x+ y|p ≤ (|x|+ |y|)p ≤ 2p−1 (|x|p + |y|p) ■

Note that if y = φ (x) is any function for which the graph of φ is concave up, you couldget a similar inequality by the same argument.

Corollary 12.1.5 (Minkowski inequality) Let 1≤ p < ∞. Then(∫| f +g|p dµ

)1/p

≤(∫| f |p dµ

)1/p

+

(∫|g|p dµ

)1/p

. (12.2)

Proof: If p = 1, this is obvious. Let p > 1. Without loss of generality, assume(∫| f |p dµ)1/p+(

∫|g|p dµ)1/p < ∞ and (

∫| f +g|p dµ)1/p ̸= 0 or there is nothing to prove.

Therefore, using the above lemma,∫| f +g|pdµ ≤ 2p−1

(∫| f |p + |g|pdµ

)< ∞.

Now | f (ω)+g(ω)|p ≤ | f (ω)+g(ω)|p−1 (| f (ω)|+ |g(ω)|) . Also, it follows from thedefinition of p and q that p−1 = p

q . Therefore, using this and Holder’s inequality,∫| f +

g|pdµ ≤ ∫| f +g|p−1| f |dµ +

∫| f +g|p−1|g|dµ =

∫| f +g|

pq | f |dµ +

∫| f +g|

pq |g|dµ

≤ (∫| f +g|pdµ)

1q (∫| f |pdµ)

1p +(

∫| f +g|pdµ)

1q (∫|g|pdµ)

1p.

Dividing both sides by (∫| f +g|pdµ)

1q yields 12.2. ■

The above theorem implies the following corollary.

Corollary 12.1.6 Let fi ∈ Lp (Ω) for i = 1,2, · · · ,n. Then(∫ ∣∣∣∣∣ n

∑i=1

fi

∣∣∣∣∣p

dµ

)1/p

≤n

∑i=1

(∫| fi|p

)1/p

.

This shows that if f ,g ∈ Lp, then f +g ∈ Lp. Also, it is clear that if a is a constant andf ∈ Lp, then a f ∈ Lp because

∫|a f |p dµ = |a|p

∫| f |p dµ < ∞. Thus Lp is a vector space

anda.) (

∫| f |p dµ)1/p ≥ 0,(

∫| f |p dµ)1/p = 0 if and only if f = 0 a.e.