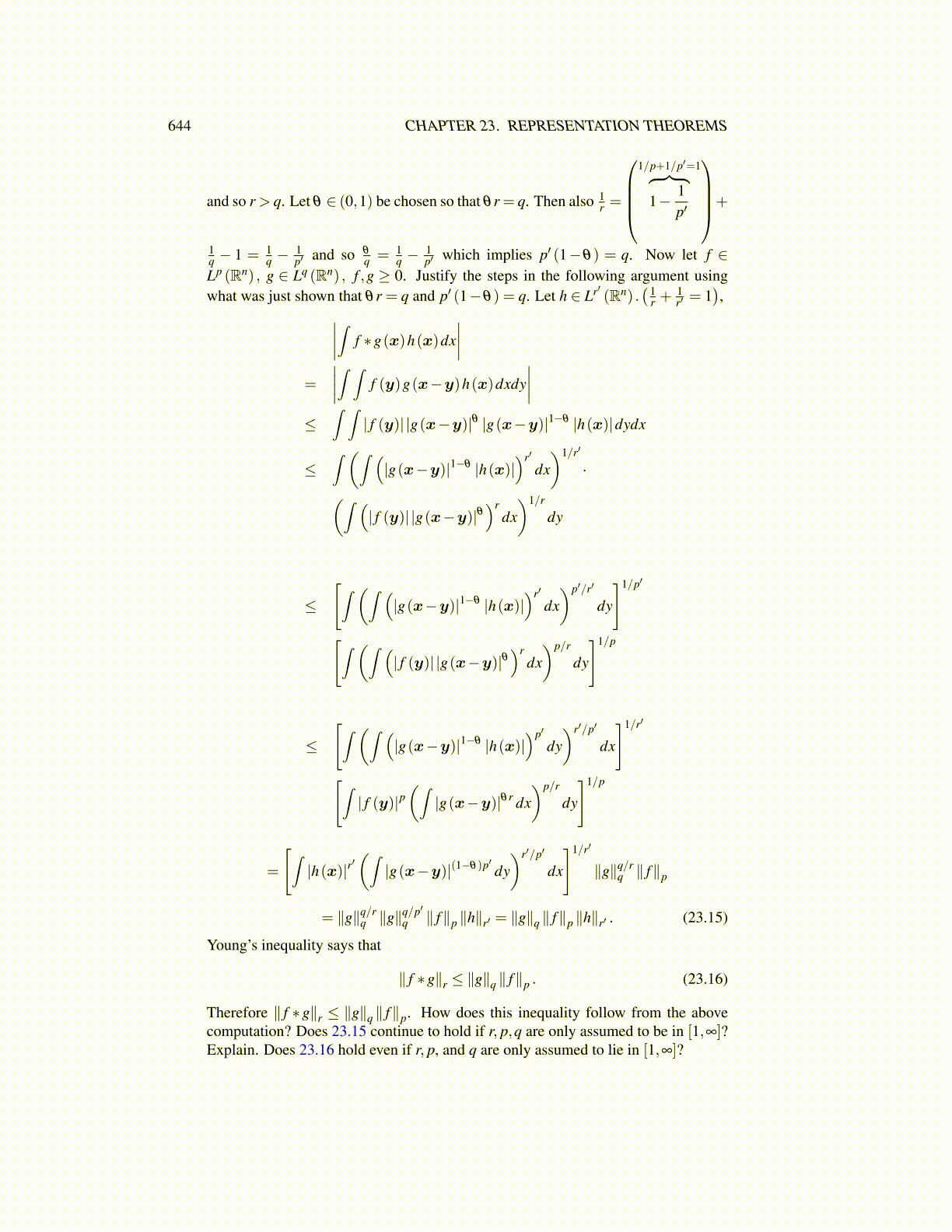
644 CHAPTER 23. REPRESENTATION THEOREMS
and so r > q. Let θ ∈ (0,1) be chosen so that θr = q. Then also 1r =
1/p+1/p′=1︷ ︸︸ ︷
1− 1p′
+
1q − 1 = 1
q −1p′ and so θ
q = 1q −
1p′ which implies p′ (1−θ) = q. Now let f ∈
Lp (Rn) , g ∈ Lq (Rn) , f ,g ≥ 0. Justify the steps in the following argument usingwhat was just shown that θr = q and p′ (1−θ) = q. Let h ∈ Lr′ (Rn) .
( 1r +
1r′ = 1
),∣∣∣∣∫ f ∗g(x)h(x)dx
∣∣∣∣=
∣∣∣∣∫ ∫ f (y)g(x−y)h(x)dxdy∣∣∣∣
≤∫ ∫
| f (y)| |g(x−y)|θ |g(x−y)|1−θ |h(x)|dydx
≤∫ (∫ (
|g(x−y)|1−θ |h(x)|)r′
dx)1/r′
·(∫ (| f (y)| |g(x−y)|θ
)rdx)1/r
dy
≤
[∫ (∫ (|g(x−y)|1−θ |h(x)|
)r′
dx)p′/r′
dy
]1/p′
[∫ (∫ (| f (y)| |g(x−y)|θ
)rdx)p/r
dy
]1/p
≤
[∫ (∫ (|g(x−y)|1−θ |h(x)|
)p′
dy)r′/p′
dx
]1/r′
[∫| f (y)|p
(∫|g(x−y)|θr dx
)p/r
dy
]1/p
=
[∫|h(x)|r
′(∫|g(x−y)|(1−θ)p′ dy
)r′/p′
dx
]1/r′
∥g∥q/rq ∥ f∥p
= ∥g∥q/rq ∥g∥
q/p′q ∥ f∥p ∥h∥r′ = ∥g∥q ∥ f∥p ∥h∥r′ . (23.15)
Young’s inequality says that
∥ f ∗g∥r ≤ ∥g∥q ∥ f∥p . (23.16)
Therefore ∥ f ∗g∥r ≤ ∥g∥q ∥ f∥p. How does this inequality follow from the abovecomputation? Does 23.15 continue to hold if r, p,q are only assumed to be in [1,∞]?Explain. Does 23.16 hold even if r, p, and q are only assumed to lie in [1,∞]?