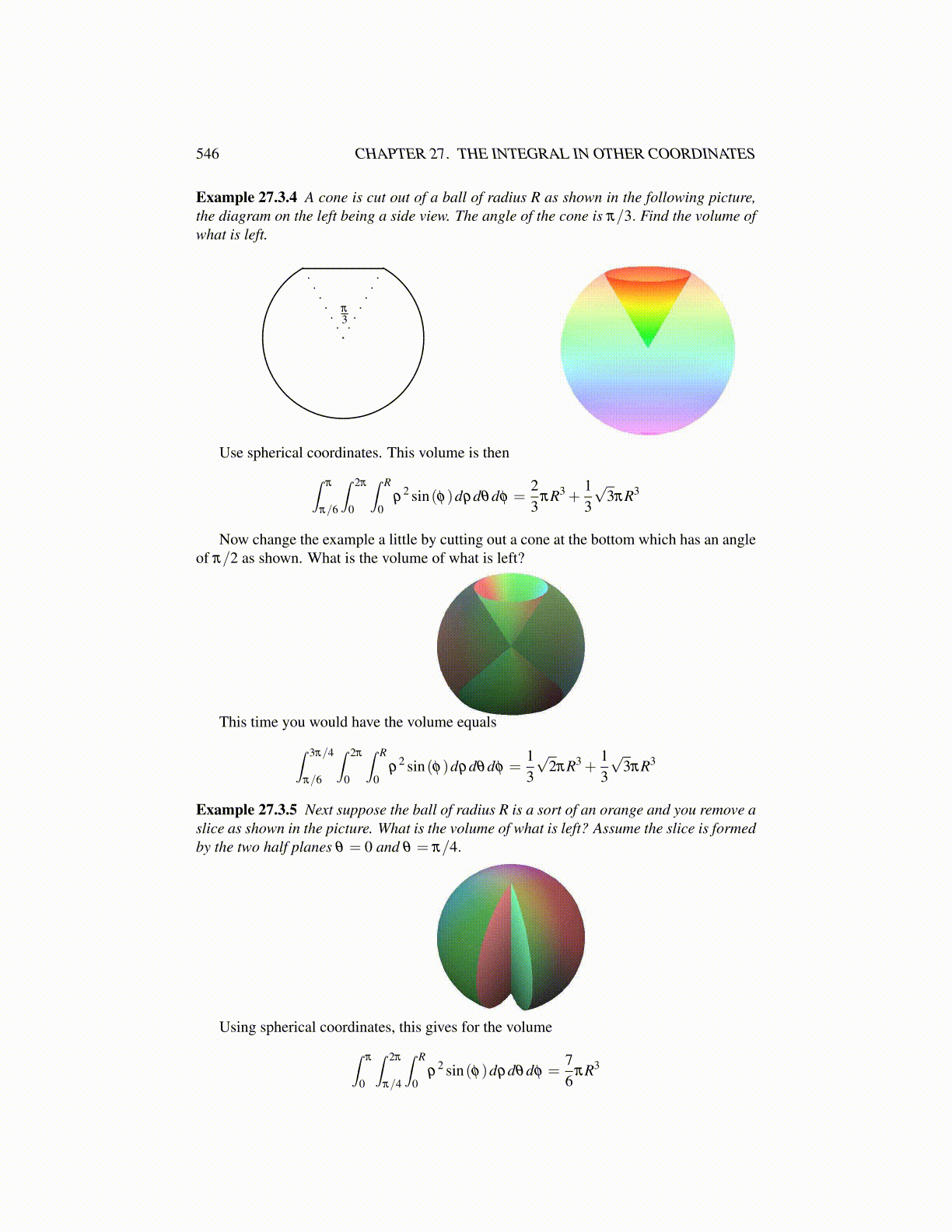
546 CHAPTER 27. THE INTEGRAL IN OTHER COORDINATES

=1

2z0

(4ρ − 2ρ

z0[(ρ + z0)− (ρ − z0)]

)= 0.

Therefore, in this case the inner integral of 27.1 equals zero and so the original integral willalso be zero.

The other case is when z0 > b and so it is always the case that z0 > ρ. In this case thefirst two terms of 27.2 are

2ρ (ρ + z0)√(ρ + z0)

2+

2ρ (ρ − z0)√(ρ − z0)

2=

2ρ (ρ + z0)

(ρ + z0)+

2ρ (ρ − z0)

z0 −ρ= 0.

Therefore in this case, 27.2 equals

12z0

−∫

π

02ρ

2 sinφ√(ρ2 + z2

0 −2ρz0 cosφ) dφ

=

−ρ

2z20

∫ π

0

2ρz0 sinφ√(ρ2 + z2

0 −2ρz0 cosφ) dφ

which equals

−ρ

z20

((ρ

2 + z20 −2ρz0 cosφ

)1/2 |π0)=

−ρ

z20[(ρ + z0)− (z0 −ρ)] =−2ρ2

z20.

Thus the inner integral of 27.1 reduces to the above simple expression. Therefore, 27.1equals ∫ 2π

0

∫ b

a

(− 2

z20

ρ2)

dρ dθ =−43

πb3 −a3

z20

and so

αGk∫

H

(z− z0)[x2 + y2 +(z− z0)

2]3/2 dV

= αGk

(−4

3π

b3 −a3

z20

)=−kG

total massz2

0.

27.4 Exercises1. Find the volume of the region bounded by z = 0,x2+(y−2)2 = 4, and z =

√x2 + y2.

2. Find the volume of the region z ≥ 0,x2 + y2 ≤ 4, and z ≤ 4−√

x2 + y2.