7.2. THE CAYLEY HAMILTON THEOREM∗ 139
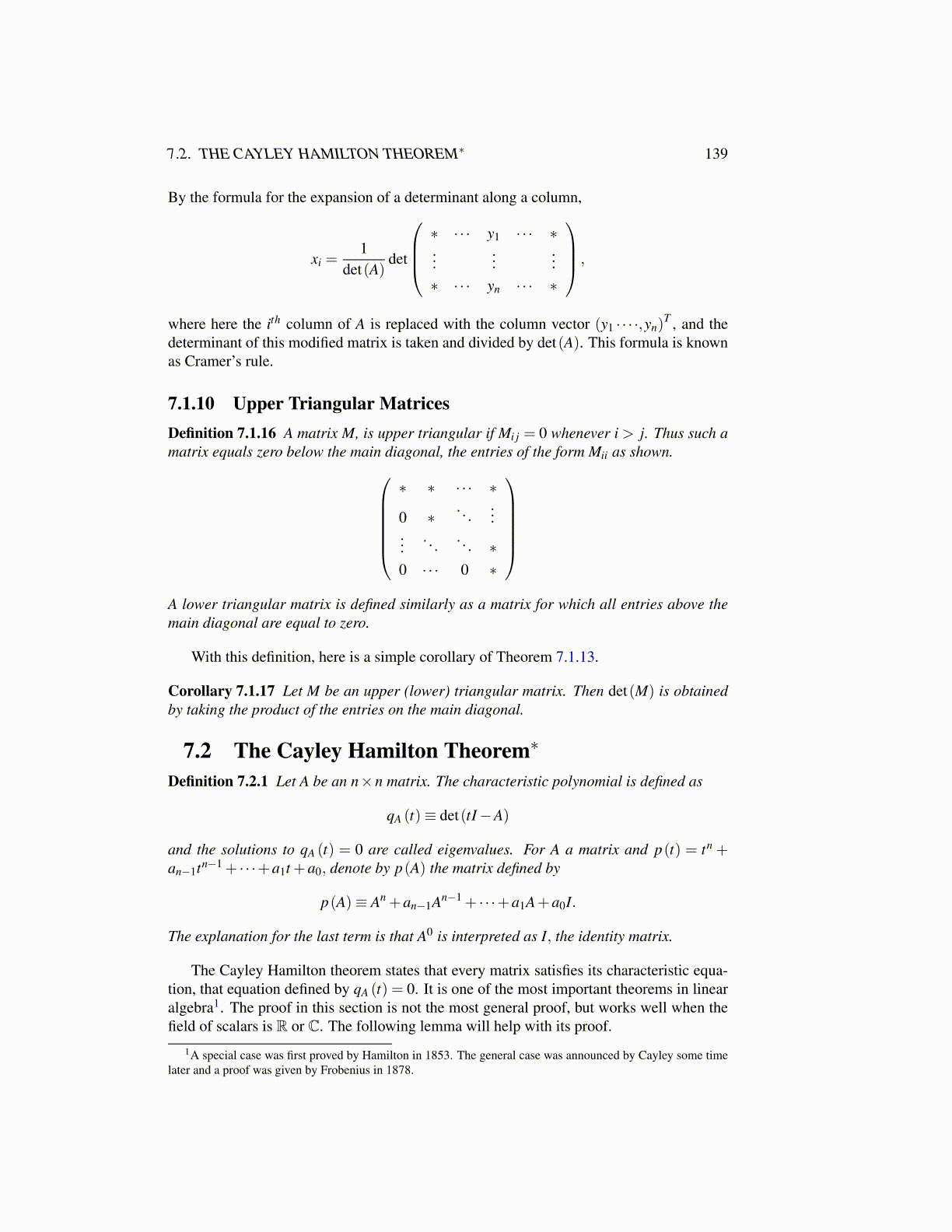
By the formula for the expansion of a determinant along a column,
xi =1
det(A)det
∗ · · · y1 · · · ∗...
......
∗ · · · yn · · · ∗
,
where here the ith column of A is replaced with the column vector (y1 · · · ·,yn)T , and the
determinant of this modified matrix is taken and divided by det(A). This formula is knownas Cramer’s rule.
7.1.10 Upper Triangular MatricesDefinition 7.1.16 A matrix M, is upper triangular if Mi j = 0 whenever i > j. Thus such amatrix equals zero below the main diagonal, the entries of the form Mii as shown.
∗ ∗ · · · ∗
0 ∗. . .
......
. . .. . . ∗
0 · · · 0 ∗
A lower triangular matrix is defined similarly as a matrix for which all entries above themain diagonal are equal to zero.
With this definition, here is a simple corollary of Theorem 7.1.13.
Corollary 7.1.17 Let M be an upper (lower) triangular matrix. Then det(M) is obtainedby taking the product of the entries on the main diagonal.
7.2 The Cayley Hamilton Theorem∗
Definition 7.2.1 Let A be an n×n matrix. The characteristic polynomial is defined as
qA (t)≡ det(tI−A)
and the solutions to qA (t) = 0 are called eigenvalues. For A a matrix and p(t) = tn +an−1tn−1 + · · ·+a1t +a0, denote by p(A) the matrix defined by
p(A)≡ An +an−1An−1 + · · ·+a1A+a0I.
The explanation for the last term is that A0 is interpreted as I, the identity matrix.
The Cayley Hamilton theorem states that every matrix satisfies its characteristic equa-tion, that equation defined by qA (t) = 0. It is one of the most important theorems in linearalgebra1. The proof in this section is not the most general proof, but works well when thefield of scalars is R or C. The following lemma will help with its proof.
1A special case was first proved by Hamilton in 1853. The general case was announced by Cayley some timelater and a proof was given by Frobenius in 1878.