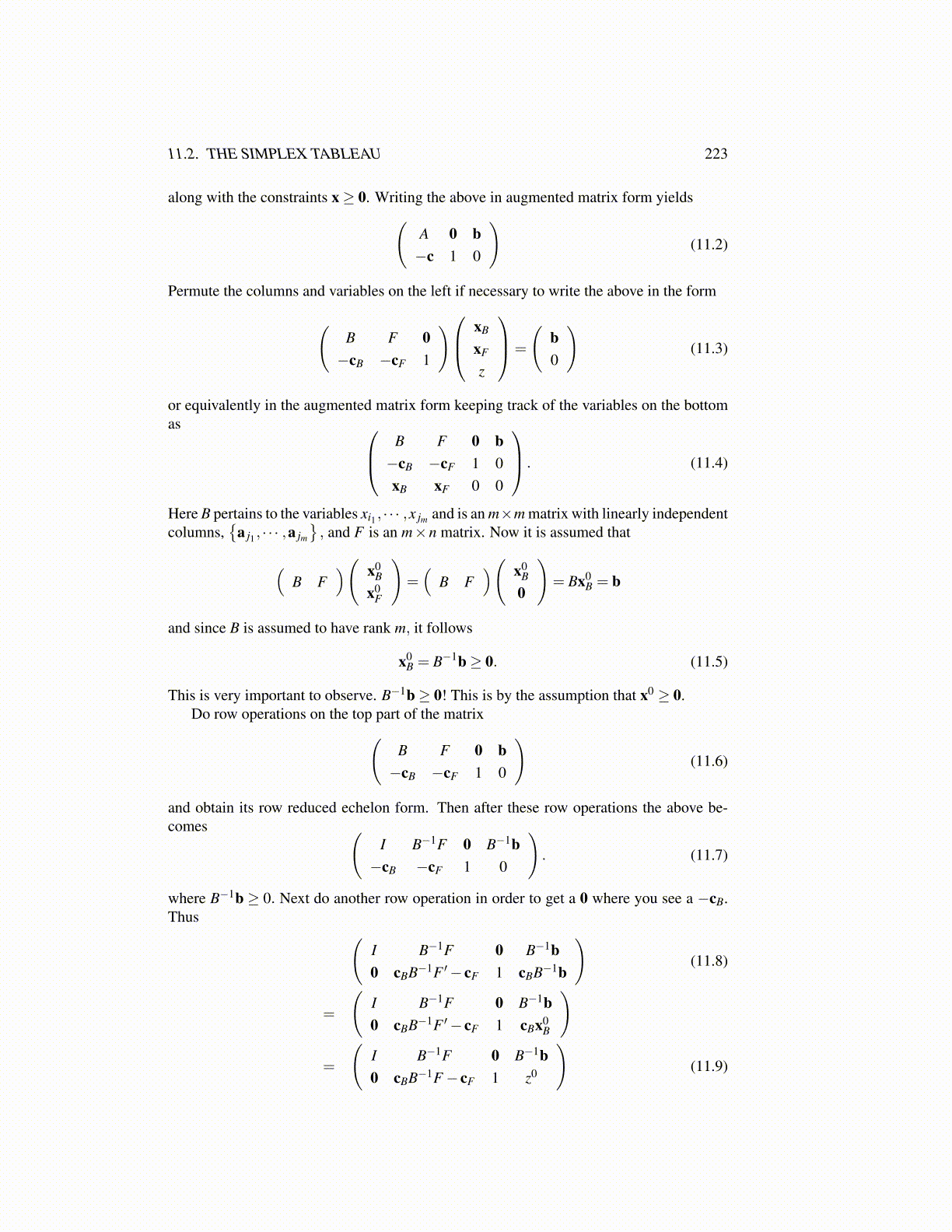
11.2. THE SIMPLEX TABLEAU 223

along with the constraints x≥ 0. Writing the above in augmented matrix form yields(A 0 b−c 1 0

)(11.2)

Permute the columns and variables on the left if necessary to write the above in the form

(B F 0−cB −cF 1

) xB

xF

z

=

(b0

)(11.3)

or equivalently in the augmented matrix form keeping track of the variables on the bottomas  B F 0 b

−cB −cF 1 0xB xF 0 0

 . (11.4)

Here B pertains to the variables xi1 , · · · ,x jm and is an m×m matrix with linearly independentcolumns,

{a j1 , · · · ,a jm

}, and F is an m×n matrix. Now it is assumed that

(B F

)( x0B

x0F

)=(

B F)( x0

B

0

)= Bx0

B = b

and since B is assumed to have rank m, it follows

x0B = B−1b≥ 0. (11.5)

This is very important to observe. B−1b≥ 0! This is by the assumption that x0 ≥ 0.Do row operations on the top part of the matrix(

B F 0 b−cB −cF 1 0

)(11.6)

and obtain its row reduced echelon form. Then after these row operations the above be-comes (

I B−1F 0 B−1b−cB −cF 1 0

). (11.7)

where B−1b ≥ 0. Next do another row operation in order to get a 0 where you see a −cB.Thus (

I B−1F 0 B−1b0 cBB−1F ′− cF 1 cBB−1b

)(11.8)

=

(I B−1F 0 B−1b0 cBB−1F ′− cF 1 cBx0

B

)

=

(I B−1F 0 B−1b0 cBB−1F− cF 1 z0

)(11.9)