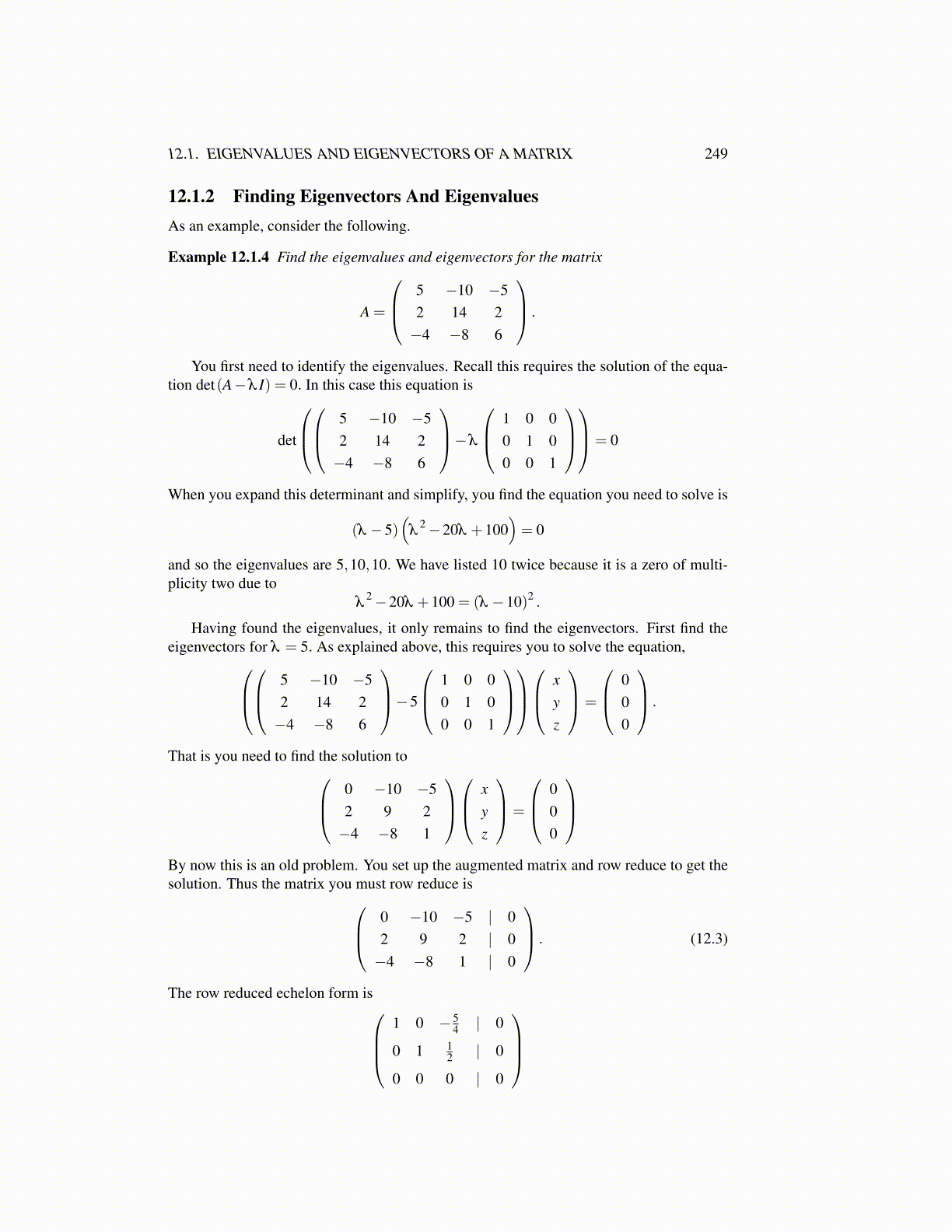
12.1. EIGENVALUES AND EIGENVECTORS OF A MATRIX 249
12.1.2 Finding Eigenvectors And EigenvaluesAs an example, consider the following.
Example 12.1.4 Find the eigenvalues and eigenvectors for the matrix
A =
5 −10 −52 14 2−4 −8 6
.
You first need to identify the eigenvalues. Recall this requires the solution of the equa-tion det(A−λ I) = 0. In this case this equation is
det
5 −10 −5
2 14 2−4 −8 6
−λ
1 0 00 1 00 0 1
= 0
When you expand this determinant and simplify, you find the equation you need to solve is
(λ −5)(
λ2−20λ +100
)= 0
and so the eigenvalues are 5,10,10. We have listed 10 twice because it is a zero of multi-plicity two due to
λ2−20λ +100 = (λ −10)2 .
Having found the eigenvalues, it only remains to find the eigenvectors. First find theeigenvectors for λ = 5. As explained above, this requires you to solve the equation,
5 −10 −52 14 2−4 −8 6
−5
1 0 00 1 00 0 1
x
yz
=
000
.
That is you need to find the solution to 0 −10 −52 9 2−4 −8 1
x
yz
=
000
By now this is an old problem. You set up the augmented matrix and row reduce to get thesolution. Thus the matrix you must row reduce is 0 −10 −5 | 0
2 9 2 | 0−4 −8 1 | 0
. (12.3)
The row reduced echelon form is1 0 − 5
4 | 0
0 1 12 | 0
0 0 0 | 0