13.2. FUNDAMENTAL THEORY AND GENERALIZATIONS 301
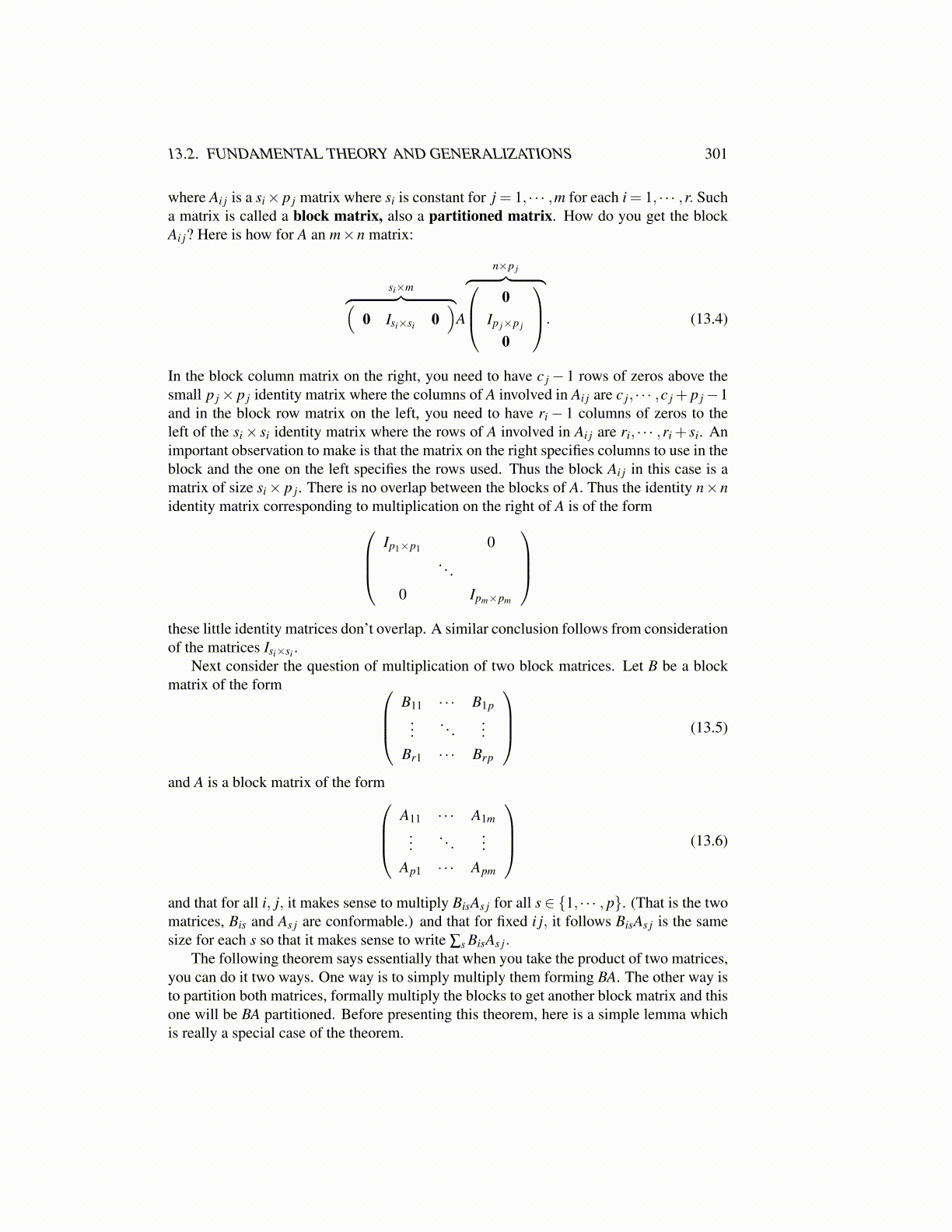
where Ai j is a si× p j matrix where si is constant for j = 1, · · · ,m for each i = 1, · · · ,r. Sucha matrix is called a block matrix, also a partitioned matrix. How do you get the blockAi j? Here is how for A an m×n matrix:
si×m︷ ︸︸ ︷(0 Isi×si 0
)A
n×p j︷ ︸︸ ︷ 0Ip j×p j
0
. (13.4)
In the block column matrix on the right, you need to have c j− 1 rows of zeros above thesmall p j× p j identity matrix where the columns of A involved in Ai j are c j, · · · ,c j + p j−1and in the block row matrix on the left, you need to have ri− 1 columns of zeros to theleft of the si× si identity matrix where the rows of A involved in Ai j are ri, · · · ,ri + si. Animportant observation to make is that the matrix on the right specifies columns to use in theblock and the one on the left specifies the rows used. Thus the block Ai j in this case is amatrix of size si× p j. There is no overlap between the blocks of A. Thus the identity n×nidentity matrix corresponding to multiplication on the right of A is of the form
Ip1×p1 0. . .
0 Ipm×pm
these little identity matrices don’t overlap. A similar conclusion follows from considerationof the matrices Isi×si .
Next consider the question of multiplication of two block matrices. Let B be a blockmatrix of the form
B11 · · · B1p...
. . ....
Br1 · · · Brp
(13.5)
and A is a block matrix of the formA11 · · · A1m
.... . .
...Ap1 · · · Apm
(13.6)
and that for all i, j, it makes sense to multiply BisAs j for all s ∈ {1, · · · , p}. (That is the twomatrices, Bis and As j are conformable.) and that for fixed i j, it follows BisAs j is the samesize for each s so that it makes sense to write ∑s BisAs j.
The following theorem says essentially that when you take the product of two matrices,you can do it two ways. One way is to simply multiply them forming BA. The other way isto partition both matrices, formally multiply the blocks to get another block matrix and thisone will be BA partitioned. Before presenting this theorem, here is a simple lemma whichis really a special case of the theorem.