74 CHAPTER 4. SYSTEMS OF EQUATIONS

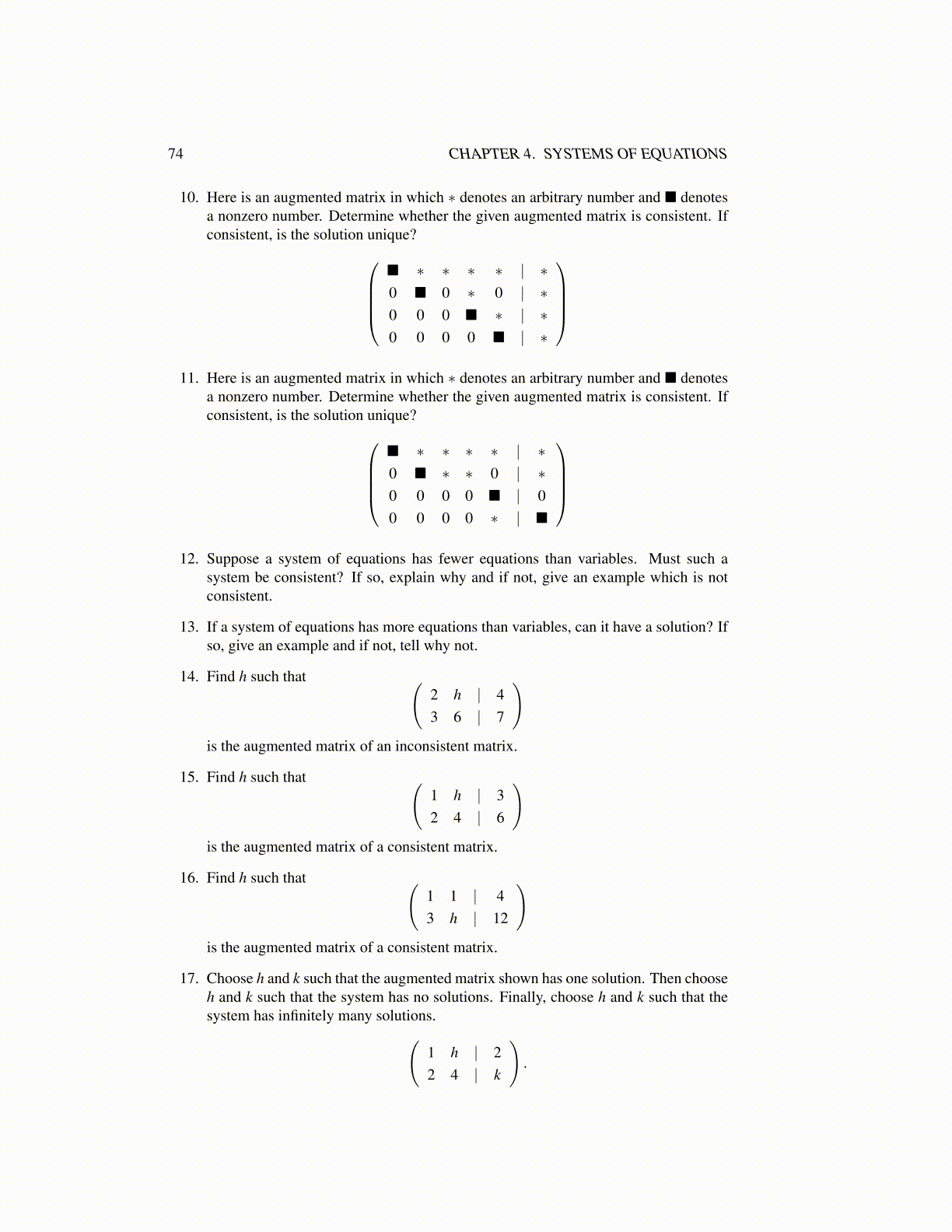
10. Here is an augmented matrix in which ∗ denotes an arbitrary number and ■ denotesa nonzero number. Determine whether the given augmented matrix is consistent. Ifconsistent, is the solution unique?

■ ∗ ∗ ∗ ∗ | ∗0 ■ 0 ∗ 0 | ∗0 0 0 ■ ∗ | ∗0 0 0 0 ■ | ∗

11. Here is an augmented matrix in which ∗ denotes an arbitrary number and ■ denotes

a nonzero number. Determine whether the given augmented matrix is consistent. Ifconsistent, is the solution unique?

■ ∗ ∗ ∗ ∗ | ∗0 ■ ∗ ∗ 0 | ∗0 0 0 0 ■ | 00 0 0 0 ∗ | ■

12. Suppose a system of equations has fewer equations than variables. Must such a

system be consistent? If so, explain why and if not, give an example which is notconsistent.

13. If a system of equations has more equations than variables, can it have a solution? Ifso, give an example and if not, tell why not.

14. Find h such that (2 h | 43 6 | 7

)is the augmented matrix of an inconsistent matrix.

15. Find h such that (1 h | 32 4 | 6

)is the augmented matrix of a consistent matrix.

16. Find h such that (1 1 | 43 h | 12

)is the augmented matrix of a consistent matrix.

17. Choose h and k such that the augmented matrix shown has one solution. Then chooseh and k such that the system has no solutions. Finally, choose h and k such that thesystem has infinitely many solutions.(

1 h | 22 4 | k

).