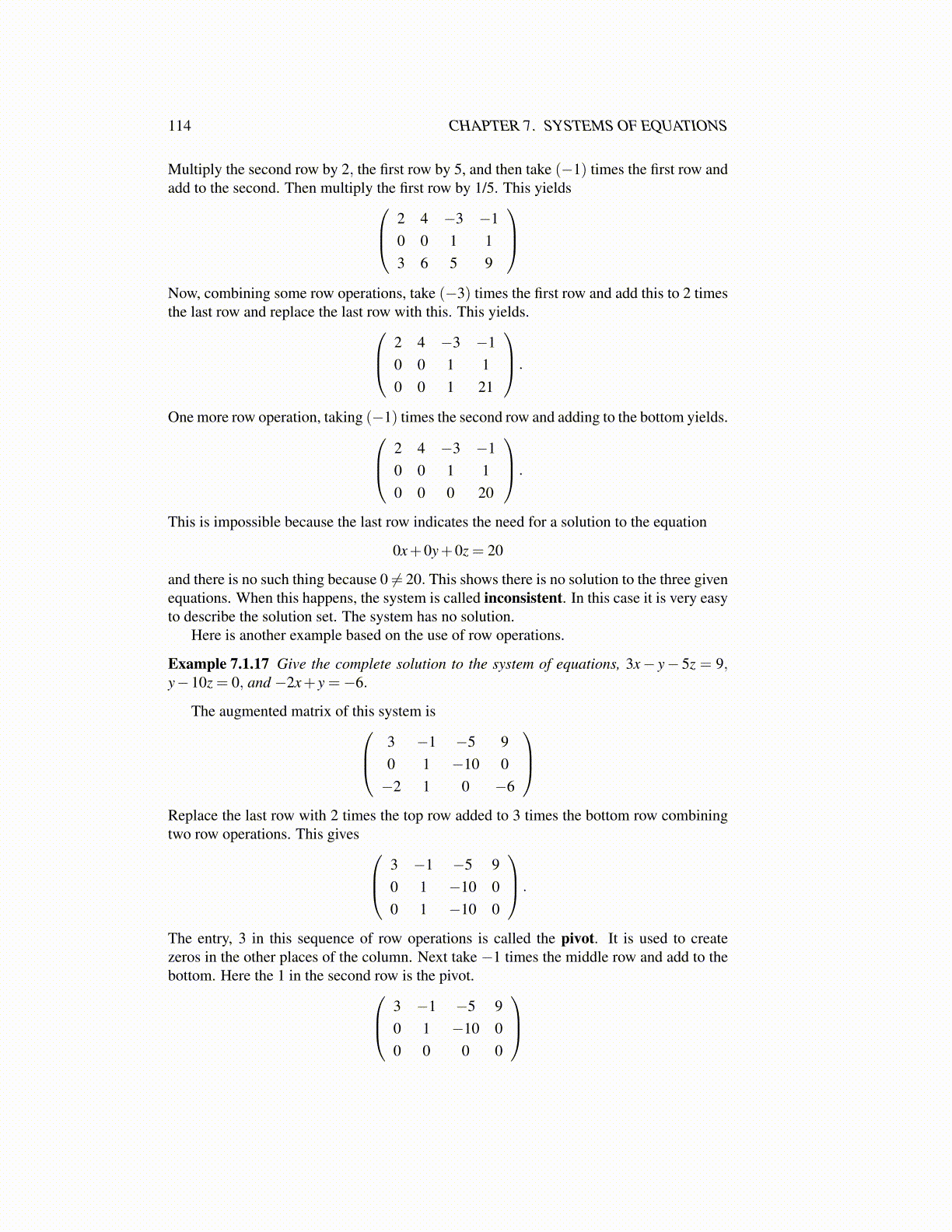
114 CHAPTER 7. SYSTEMS OF EQUATIONS

Multiply the second row by 2, the first row by 5, and then take (−1) times the first row andadd to the second. Then multiply the first row by 1/5. This yields 2 4 −3 −1

0 0 1 13 6 5 9

Now, combining some row operations, take (−3) times the first row and add this to 2 timesthe last row and replace the last row with this. This yields. 2 4 −3 −1

0 0 1 10 0 1 21

 .

One more row operation, taking (−1) times the second row and adding to the bottom yields. 2 4 −3 −10 0 1 10 0 0 20

 .

This is impossible because the last row indicates the need for a solution to the equation

0x+0y+0z = 20

and there is no such thing because 0 ̸= 20. This shows there is no solution to the three givenequations. When this happens, the system is called inconsistent. In this case it is very easyto describe the solution set. The system has no solution.

Here is another example based on the use of row operations.

Example 7.1.17 Give the complete solution to the system of equations, 3x− y− 5z = 9,y−10z = 0, and −2x+ y =−6.

The augmented matrix of this system is 3 −1 −5 90 1 −10 0−2 1 0 −6

Replace the last row with 2 times the top row added to 3 times the bottom row combiningtwo row operations. This gives  3 −1 −5 9

0 1 −10 00 1 −10 0

 .

The entry, 3 in this sequence of row operations is called the pivot. It is used to createzeros in the other places of the column. Next take −1 times the middle row and add to thebottom. Here the 1 in the second row is the pivot. 3 −1 −5 9

0 1 −10 00 0 0 0

