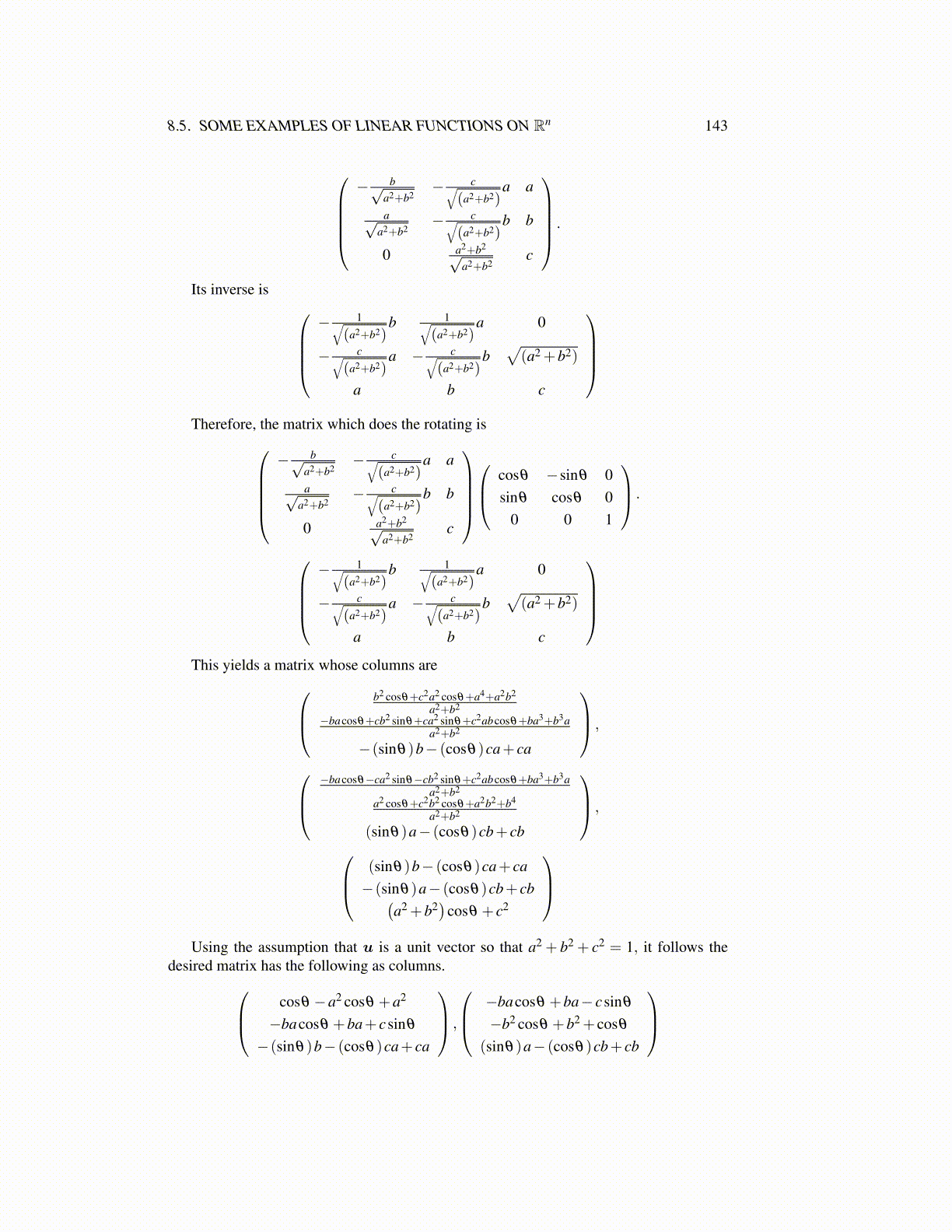
8.5. SOME EXAMPLES OF LINEAR FUNCTIONS ON Rn 143
− b√
a2+b2− c√
(a2+b2)a a
a√a2+b2
− c√(a2+b2)
b b
0 a2+b2√a2+b2
c
.
Its inverse is − 1√
(a2+b2)b 1√
(a2+b2)a 0
− c√(a2+b2)
a − c√(a2+b2)
b√
(a2 +b2)
a b c
Therefore, the matrix which does the rotating is
− b√a2+b2
− c√(a2+b2)
a a
a√a2+b2
− c√(a2+b2)
b b
0 a2+b2√a2+b2
c
cosθ −sinθ 0
sinθ cosθ 00 0 1
·− 1√
(a2+b2)b 1√
(a2+b2)a 0
− c√(a2+b2)
a − c√(a2+b2)
b√
(a2 +b2)
a b c
This yields a matrix whose columns are
b2 cosθ+c2a2 cosθ+a4+a2b2
a2+b2
−bacosθ+cb2 sinθ+ca2 sinθ+c2abcosθ+ba3+b3aa2+b2
−(sinθ)b− (cosθ)ca+ ca
,
−bacosθ−ca2 sinθ−cb2 sinθ+c2abcosθ+ba3+b3a
a2+b2
a2 cosθ+c2b2 cosθ+a2b2+b4
a2+b2
(sinθ)a− (cosθ)cb+ cb
,
(sinθ)b− (cosθ)ca+ ca−(sinθ)a− (cosθ)cb+ cb(
a2 +b2)
cosθ + c2
Using the assumption that u is a unit vector so that a2 + b2 + c2 = 1, it follows the
desired matrix has the following as columns. cosθ −a2 cosθ +a2
−bacosθ +ba+ csinθ
−(sinθ)b− (cosθ)ca+ ca
,
−bacosθ +ba− csinθ
−b2 cosθ +b2 + cosθ
(sinθ)a− (cosθ)cb+ cb