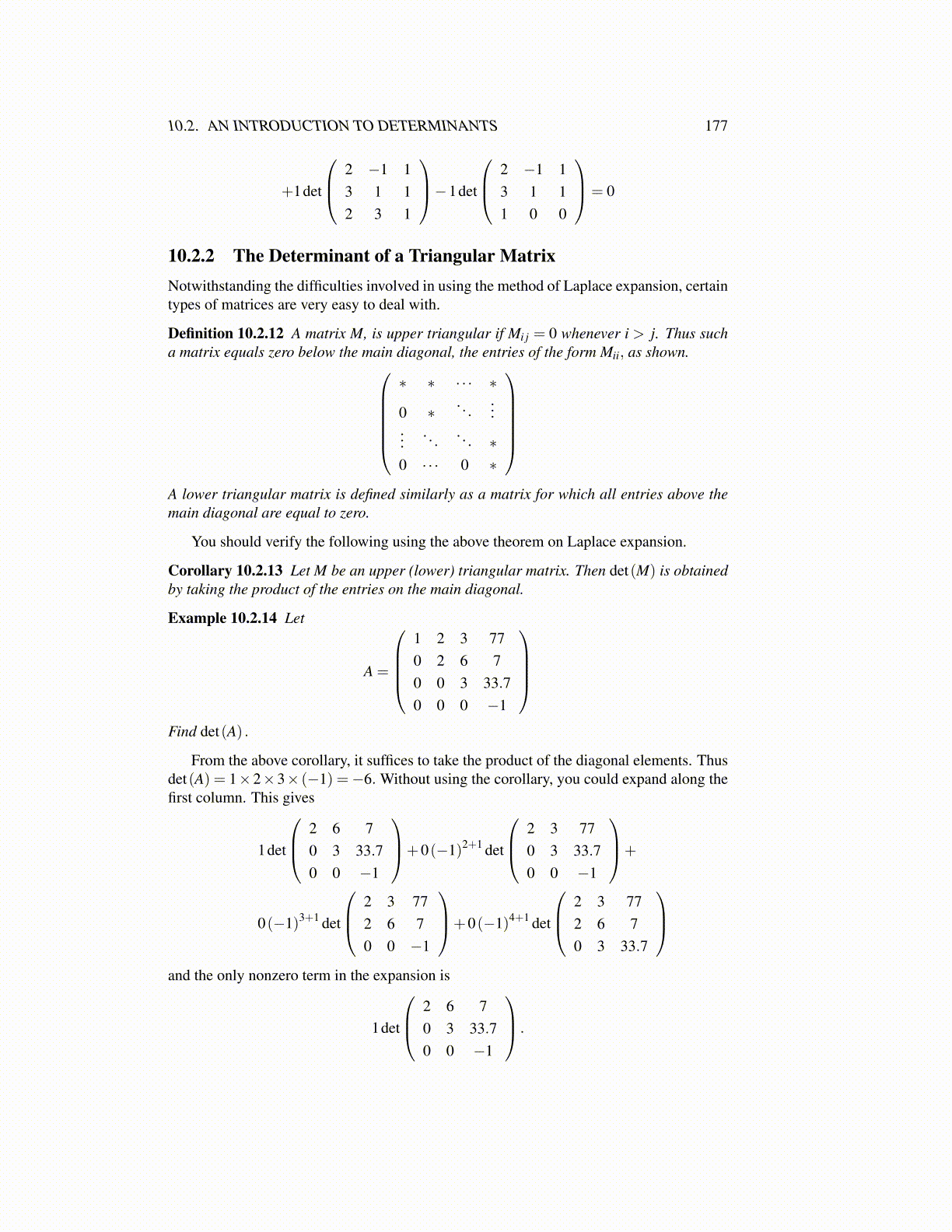
10.2. AN INTRODUCTION TO DETERMINANTS 177
+1det
2 −1 13 1 12 3 1
−1det
2 −1 13 1 11 0 0
= 0
10.2.2 The Determinant of a Triangular MatrixNotwithstanding the difficulties involved in using the method of Laplace expansion, certaintypes of matrices are very easy to deal with.
Definition 10.2.12 A matrix M, is upper triangular if Mi j = 0 whenever i > j. Thus sucha matrix equals zero below the main diagonal, the entries of the form Mii, as shown.
∗ ∗ · · · ∗
0 ∗. . .
......
. . .. . . ∗
0 · · · 0 ∗
A lower triangular matrix is defined similarly as a matrix for which all entries above themain diagonal are equal to zero.
You should verify the following using the above theorem on Laplace expansion.
Corollary 10.2.13 Let M be an upper (lower) triangular matrix. Then det(M) is obtainedby taking the product of the entries on the main diagonal.
Example 10.2.14 Let
A =
1 2 3 770 2 6 70 0 3 33.70 0 0 −1
Find det(A) .
From the above corollary, it suffices to take the product of the diagonal elements. Thusdet(A) = 1×2×3× (−1) =−6. Without using the corollary, you could expand along thefirst column. This gives
1det
2 6 70 3 33.70 0 −1
+0(−1)2+1 det
2 3 770 3 33.70 0 −1
+
0(−1)3+1 det
2 3 772 6 70 0 −1
+0(−1)4+1 det
2 3 772 6 70 3 33.7
and the only nonzero term in the expansion is
1det
2 6 70 3 33.70 0 −1
.