204 CHAPTER 11. MATRICES AND THE INNER PRODUCT

and so you need to solve (58 1818 7

)(mb

)=

(8528

)

The solution is: (91824741

)=

(1.10981.1463

)Thus the least squares line is

y = 1.1098x+1.1463

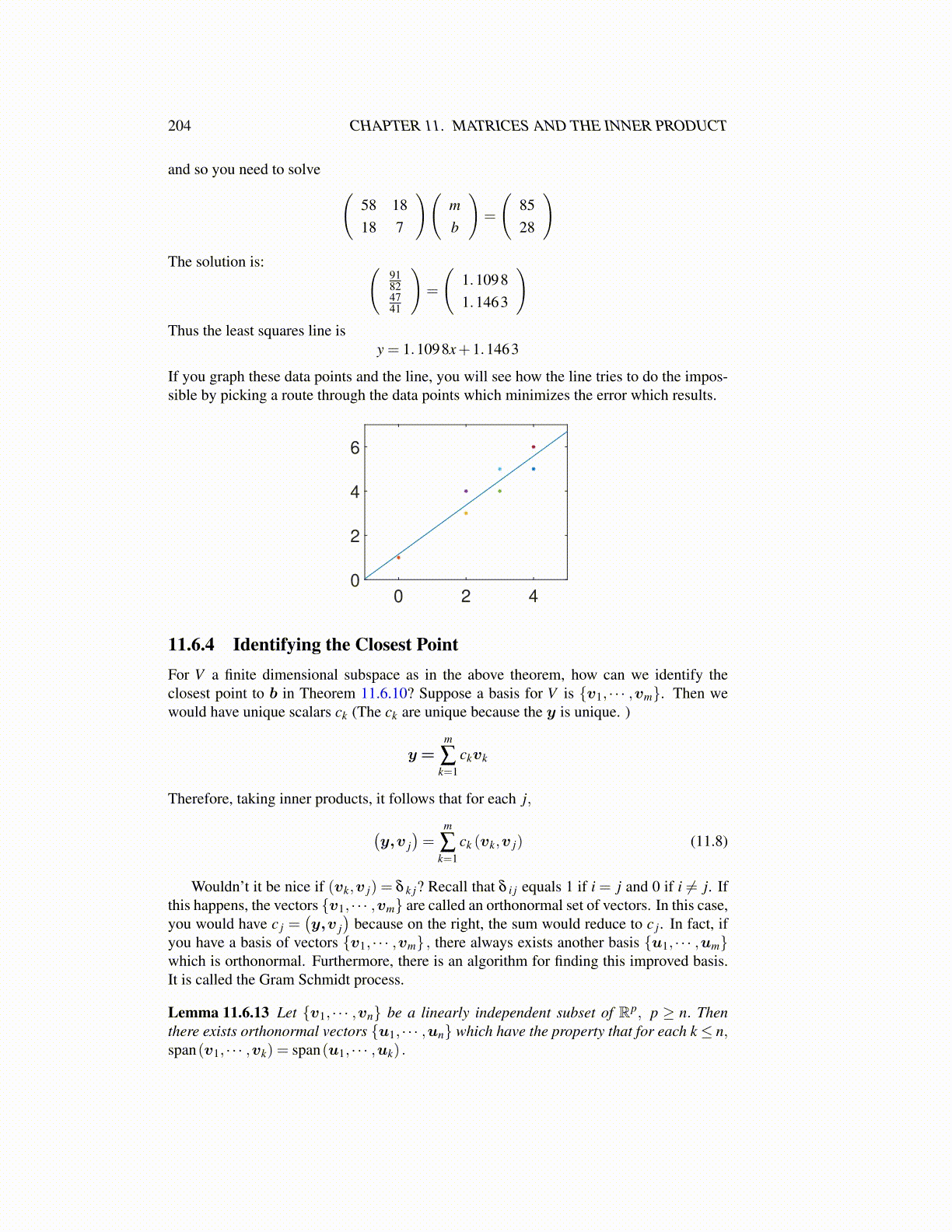
If you graph these data points and the line, you will see how the line tries to do the impos-sible by picking a route through the data points which minimizes the error which results.

0 2 40

2

4

6

11.6.4 Identifying the Closest PointFor V a finite dimensional subspace as in the above theorem, how can we identify theclosest point to b in Theorem 11.6.10? Suppose a basis for V is {v1, · · · ,vm}. Then wewould have unique scalars ck (The ck are unique because the y is unique. )

y =m

∑k=1

ckvk

Therefore, taking inner products, it follows that for each j,

(y,v j

)=

m

∑k=1

ck (vk,v j) (11.8)

Wouldn’t it be nice if (vk,v j) = δ k j? Recall that δ i j equals 1 if i = j and 0 if i ̸= j. Ifthis happens, the vectors {v1, · · · ,vm} are called an orthonormal set of vectors. In this case,you would have c j =

(y,v j

)because on the right, the sum would reduce to c j. In fact, if

you have a basis of vectors {v1, · · · ,vm} , there always exists another basis {u1, · · · ,um}which is orthonormal. Furthermore, there is an algorithm for finding this improved basis.It is called the Gram Schmidt process.

Lemma 11.6.13 Let {v1, · · · ,vn} be a linearly independent subset of Rp, p ≥ n. Thenthere exists orthonormal vectors {u1, · · · ,un} which have the property that for each k≤ n,span(v1, · · · ,vk) = span(u1, · · · ,uk) .