20.3. CYLINDRICAL AND SPHERICAL COORDINATES 371

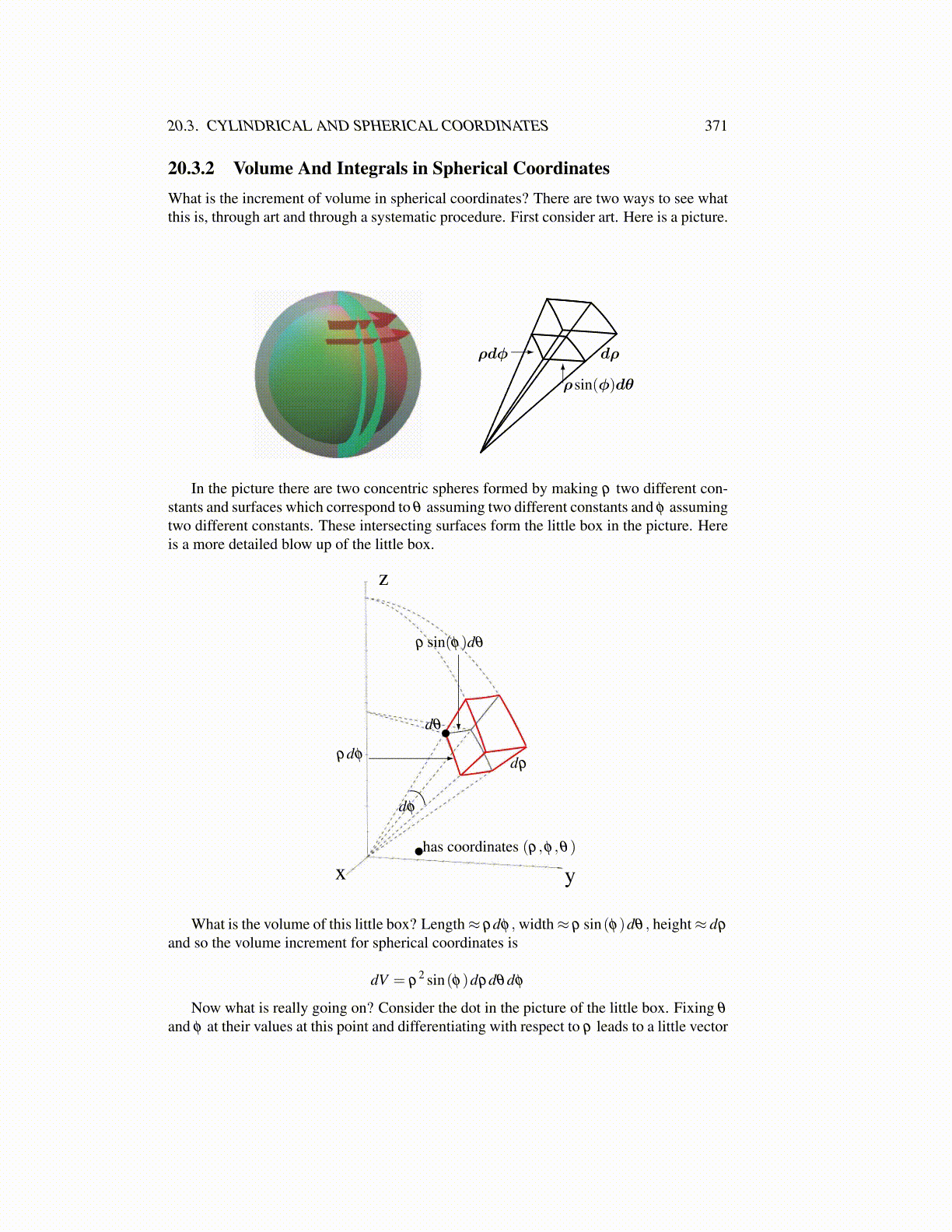
20.3.2 Volume And Integrals in Spherical CoordinatesWhat is the increment of volume in spherical coordinates? There are two ways to see whatthis is, through art and through a systematic procedure. First consider art. Here is a picture.

dρρdϕ

ρsin(ϕ)dθ

In the picture there are two concentric spheres formed by making ρ two different con-stants and surfaces which correspond to θ assuming two different constants and φ assumingtwo different constants. These intersecting surfaces form the little box in the picture. Hereis a more detailed blow up of the little box.

dφ

dθ

dρρdφ

ρ sin(φ)dθ

has coordinates (ρ,φ ,θ)

z

x y

What is the volume of this little box? Length≈ ρdφ , width≈ ρ sin(φ)dθ , height≈ dρ

and so the volume increment for spherical coordinates is

dV = ρ2 sin(φ)dρdθdφ

Now what is really going on? Consider the dot in the picture of the little box. Fixing θ

and φ at their values at this point and differentiating with respect to ρ leads to a little vector