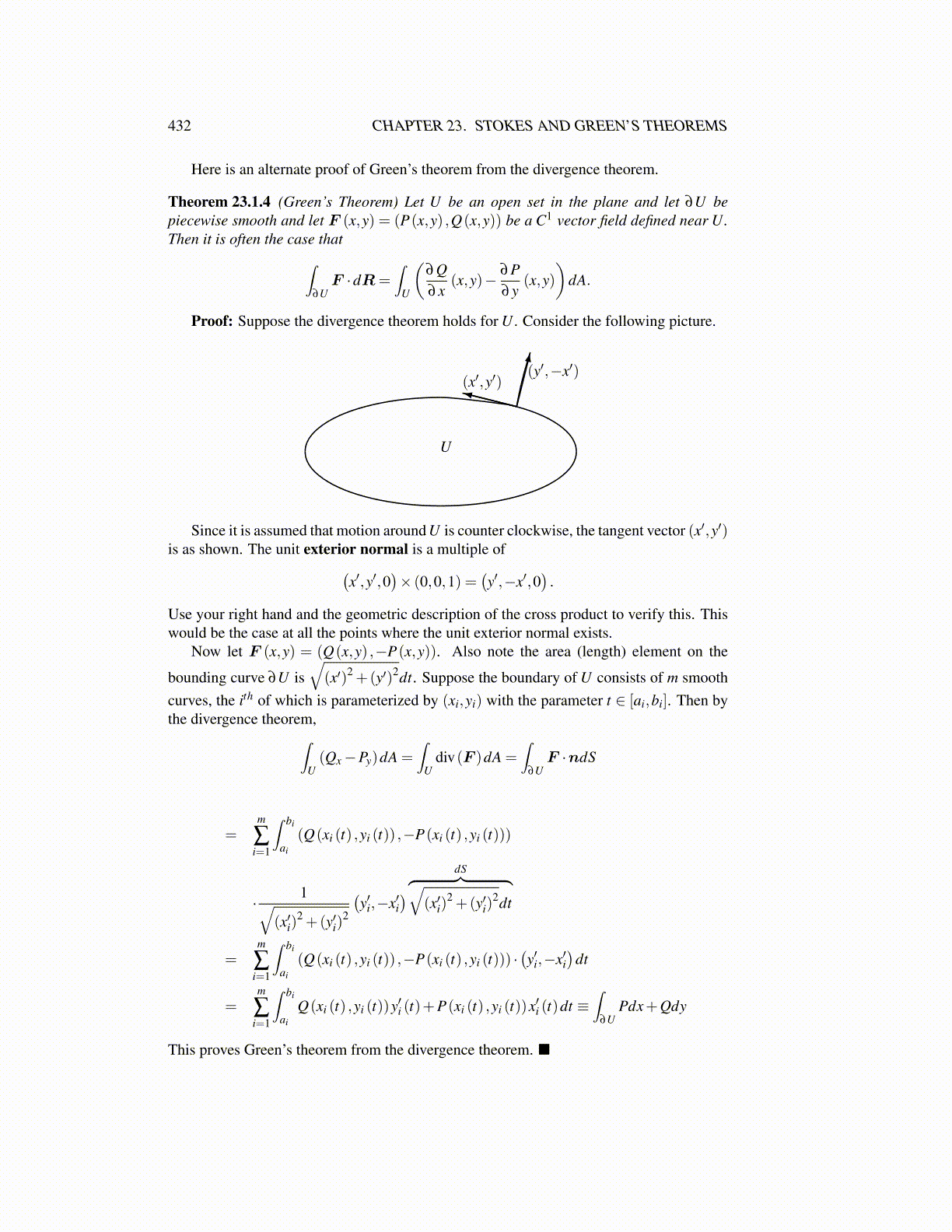
432 CHAPTER 23. STOKES AND GREEN’S THEOREMS

Here is an alternate proof of Green’s theorem from the divergence theorem.

Theorem 23.1.4 (Green’s Theorem) Let U be an open set in the plane and let ∂U bepiecewise smooth and let F (x,y) = (P(x,y) ,Q(x,y)) be a C1 vector field defined near U.Then it is often the case that∫

∂UF ·dR=

∫U

(∂Q∂x

(x,y)− ∂P∂y

(x,y))

dA.

Proof: Suppose the divergence theorem holds for U . Consider the following picture.

(x′,y′)(y′,−x′)

U

Since it is assumed that motion around U is counter clockwise, the tangent vector (x′,y′)is as shown. The unit exterior normal is a multiple of(

x′,y′,0)× (0,0,1) =

(y′,−x′,0

).

Use your right hand and the geometric description of the cross product to verify this. Thiswould be the case at all the points where the unit exterior normal exists.

Now let F (x,y) = (Q(x,y) ,−P(x,y)). Also note the area (length) element on the

bounding curve ∂U is√

(x′)2 +(y′)2dt. Suppose the boundary of U consists of m smoothcurves, the ith of which is parameterized by (xi,yi) with the parameter t ∈ [ai,bi]. Then bythe divergence theorem,∫

U(Qx−Py)dA =

∫U

div(F )dA =∫

∂UF ·ndS

=m

∑i=1

∫ bi

ai

(Q(xi (t) ,yi (t)) ,−P(xi (t) ,yi (t)))

· 1√(x′i)

2 +(y′i)2

(y′i,−x′i

) dS︷ ︸︸ ︷√(x′i)

2 +(y′i)2dt

=m

∑i=1

∫ bi

ai

(Q(xi (t) ,yi (t)) ,−P(xi (t) ,yi (t))) ·(y′i,−x′i

)dt

=m

∑i=1

∫ bi

ai

Q(xi (t) ,yi (t))y′i (t)+P(xi (t) ,yi (t))x′i (t)dt ≡∫

∂UPdx+Qdy

This proves Green’s theorem from the divergence theorem. ■