474 CHAPTER 25. CURVILINEAR COORDINATES
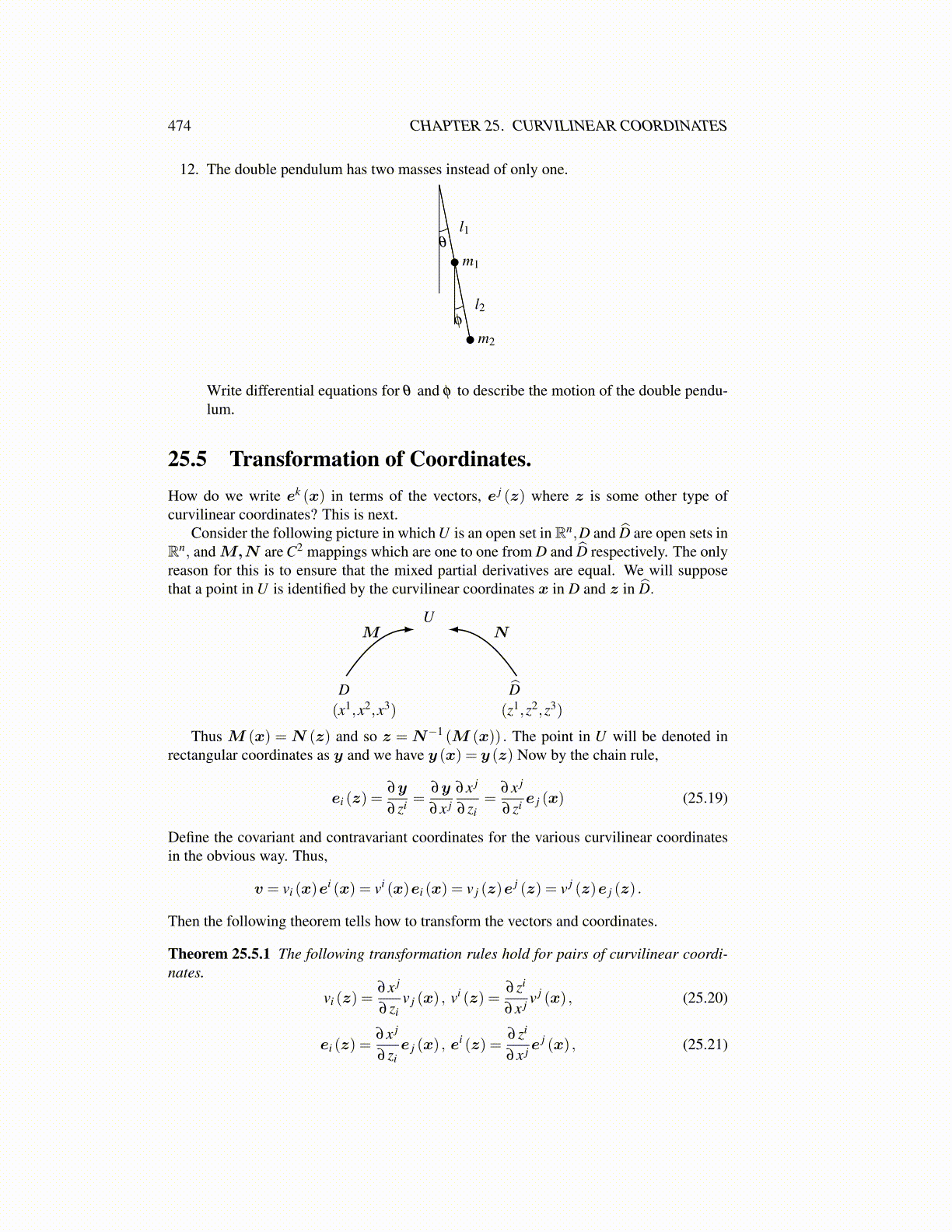
12. The double pendulum has two masses instead of only one.
m1
l1θ
m2
l2φ
Write differential equations for θ and φ to describe the motion of the double pendu-lum.
25.5 Transformation of Coordinates.How do we write ek (x) in terms of the vectors, e j (z) where z is some other type ofcurvilinear coordinates? This is next.
Consider the following picture in which U is an open set in Rn,D and D̂ are open sets inRn, and M,N are C2 mappings which are one to one from D and D̂ respectively. The onlyreason for this is to ensure that the mixed partial derivatives are equal. We will supposethat a point in U is identified by the curvilinear coordinates x in D and z in D̂.
U
D D̂
M N
(x1,x2,x3) (z1,z2,z3)
Thus M (x) = N (z) and so z = N−1 (M (x)) . The point in U will be denoted inrectangular coordinates as y and we have y (x) = y (z) Now by the chain rule,
ei (z) =∂y
∂ zi =∂y
∂x j∂x j
∂ zi=
∂x j
∂ zi e j (x) (25.19)
Define the covariant and contravariant coordinates for the various curvilinear coordinatesin the obvious way. Thus,
v = vi (x)ei (x) = vi (x)ei (x) = v j (z)e
j (z) = v j (z)e j (z) .
Then the following theorem tells how to transform the vectors and coordinates.
Theorem 25.5.1 The following transformation rules hold for pairs of curvilinear coordi-nates.
vi (z) =∂x j
∂ ziv j (x) , vi (z) =
∂ zi
∂x j v j (x) , (25.20)
ei (z) =∂x j
∂ zie j (x) , e
i (z) =∂ zi
∂x j ej (x) , (25.21)