538 CHAPTER 29. FIRST ORDER SCALAR ODE
Write the differential equation as A′ (t)+k2A(t)= 0. From Theorem 29.1.1 the solutionis
A(t) =Ce−k2t
and it only remains to find C. Letting t = 0, it follows A0 = A(0) = C. Thus A(t) =A0 exp
(−k2t
).
Now here is another problem which is a little harder because it has something extraadded in at the end.
Example 29.1.3 Find solutions to y′ = 2y+1.
Here is how you do it:
1. Write as y′−2y = 1
2. Find an “Integrating Factor”∫(−2)dt =−2t. Note that I didn’t bother to add in the
arbitrary constant. This is because it does not matter. You don’t care about findingall integrating factors. You just need one. Then an integrating factor is e−2t .
3. Multiply both sides of the equation by the integrating factor.
e−2t (y′−2y)=
ddt
(e−2ty(t)
)= e−2t (1)
Note that the first equal sign follows from the product rule and the chain rule. Thisis why we multiply by the integrating factor, to get the derivative of somethingequal to something known.
4. Take antiderivatives of both sides.
e−2ty(t) =∫
e−2tdt =−12
e−2t +C
Thusy(t) =−1
2+Ce2t
This time you need to be sure to keep the constant of integration because it doesmatter.
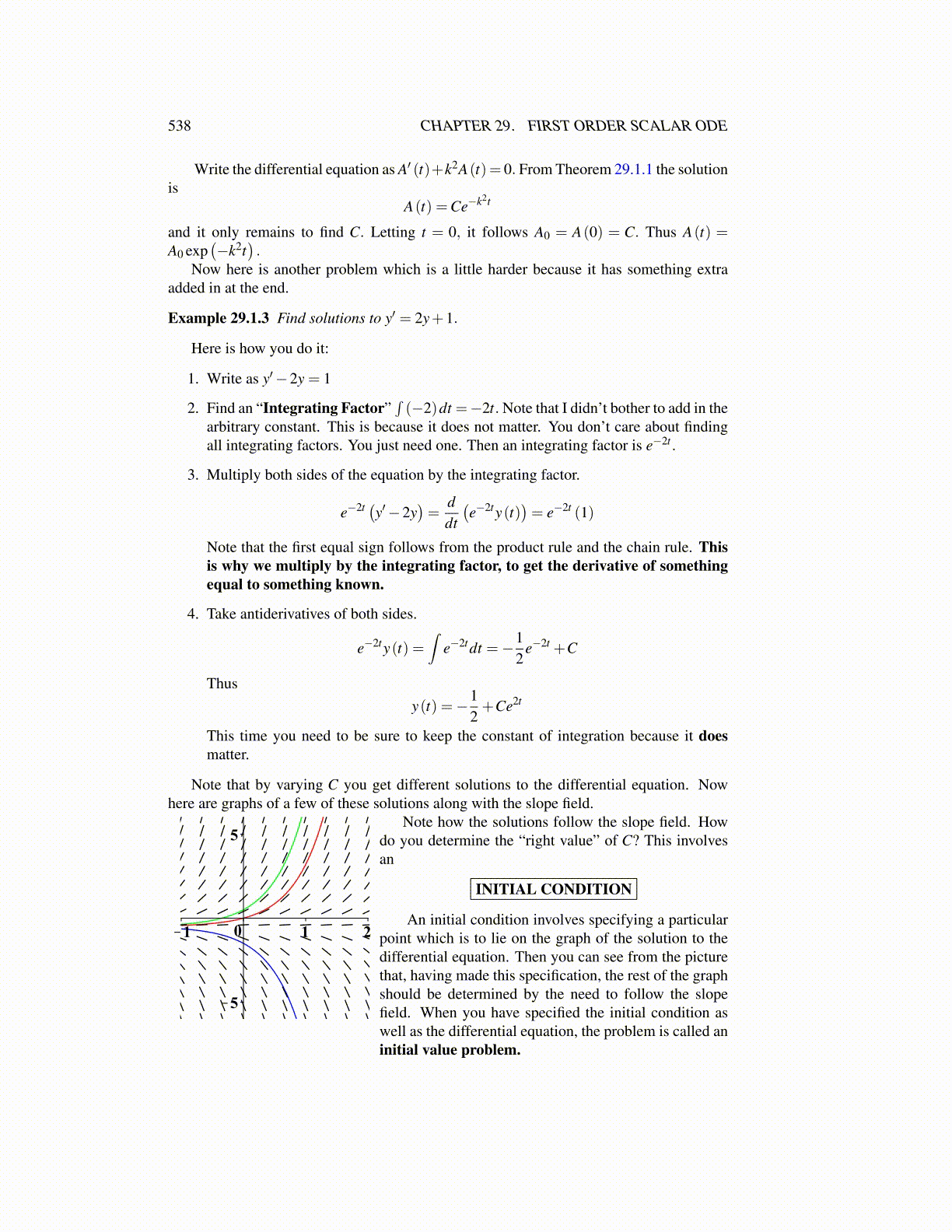
Note that by varying C you get different solutions to the differential equation. Nowhere are graphs of a few of these solutions along with the slope field.
Note how the solutions follow the slope field. Howdo you determine the “right value” of C? This involvesan
INITIAL CONDITION
An initial condition involves specifying a particularpoint which is to lie on the graph of the solution to thedifferential equation. Then you can see from the picturethat, having made this specification, the rest of the graphshould be determined by the need to follow the slopefield. When you have specified the initial condition aswell as the differential equation, the problem is called aninitial value problem.