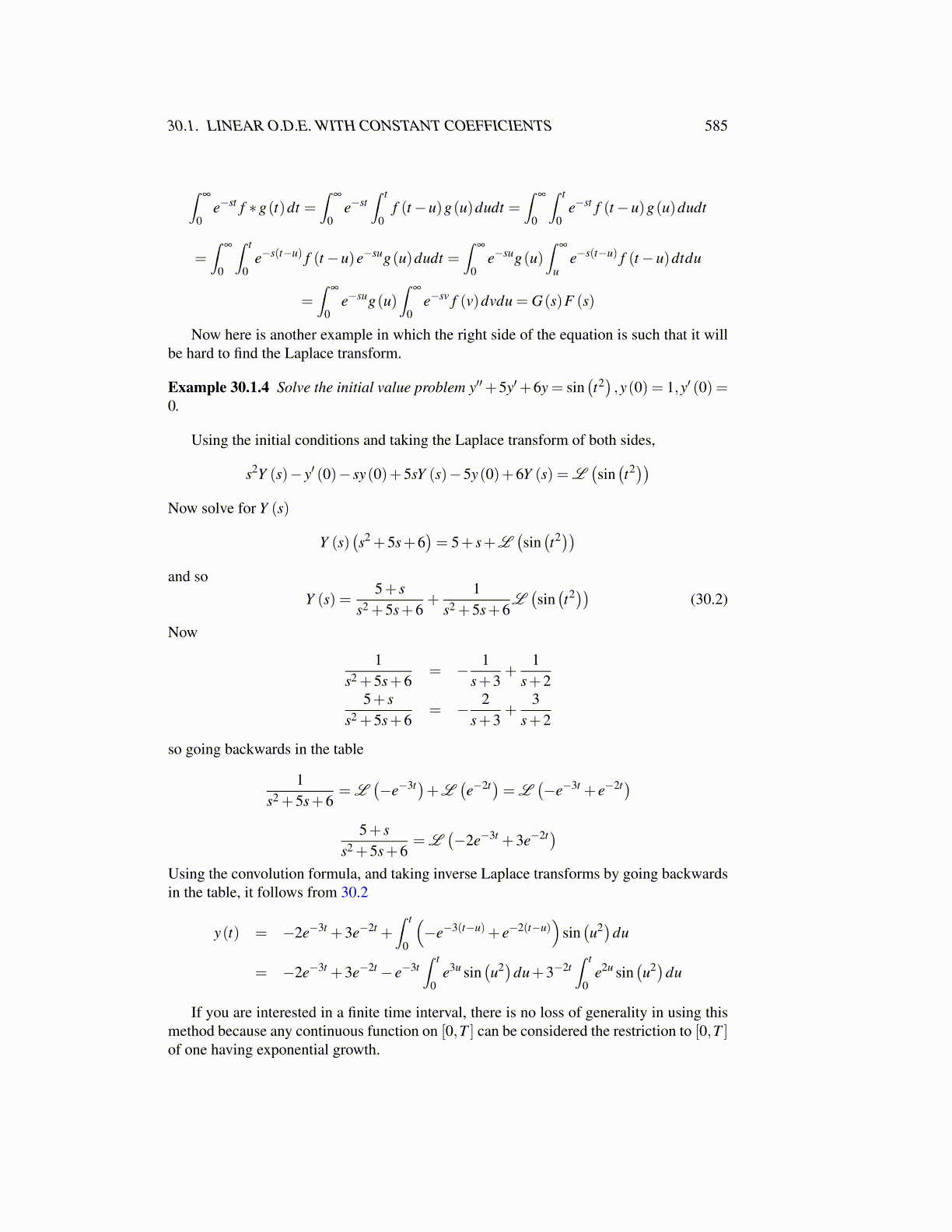
30.1. LINEAR O.D.E. WITH CONSTANT COEFFICIENTS 585

∫∞

0e−st f ∗g(t)dt =

∫∞

0e−st

∫ t

0f (t−u)g(u)dudt =

∫∞

0

∫ t

0e−st f (t−u)g(u)dudt

=∫

∞

0

∫ t

0e−s(t−u) f (t−u)e−sug(u)dudt =

∫∞

0e−sug(u)

∫∞

ue−s(t−u) f (t−u)dtdu

=∫

∞

0e−sug(u)

∫∞

0e−sv f (v)dvdu = G(s)F (s)

Now here is another example in which the right side of the equation is such that it willbe hard to find the Laplace transform.

Example 30.1.4 Solve the initial value problem y′′+5y′+6y = sin(t2),y(0) = 1,y′ (0) =

0.

Using the initial conditions and taking the Laplace transform of both sides,

s2Y (s)− y′ (0)− sy(0)+5sY (s)−5y(0)+6Y (s) = L(sin(t2))

Now solve for Y (s)

Y (s)(s2 +5s+6

)= 5+ s+L

(sin(t2))

and soY (s) =

5+ ss2 +5s+6

+1

s2 +5s+6L(sin(t2)) (30.2)

Now

1s2 +5s+6

= − 1s+3

+1

s+25+ s

s2 +5s+6= − 2

s+3+

3s+2

so going backwards in the table

1s2 +5s+6

= L(−e−3t)+L

(e−2t)= L

(−e−3t + e−2t)

5+ ss2 +5s+6

= L(−2e−3t +3e−2t)

Using the convolution formula, and taking inverse Laplace transforms by going backwardsin the table, it follows from 30.2

y(t) = −2e−3t +3e−2t +∫ t

0

(−e−3(t−u)+ e−2(t−u)

)sin(u2)du

= −2e−3t +3e−2t − e−3t∫ t

0e3u sin

(u2)du+3−2t

∫ t

0e2u sin

(u2)du

If you are interested in a finite time interval, there is no loss of generality in using thismethod because any continuous function on [0,T ] can be considered the restriction to [0,T ]of one having exponential growth.