598 CHAPTER 30. LAPLACE TRANSFORM METHODS

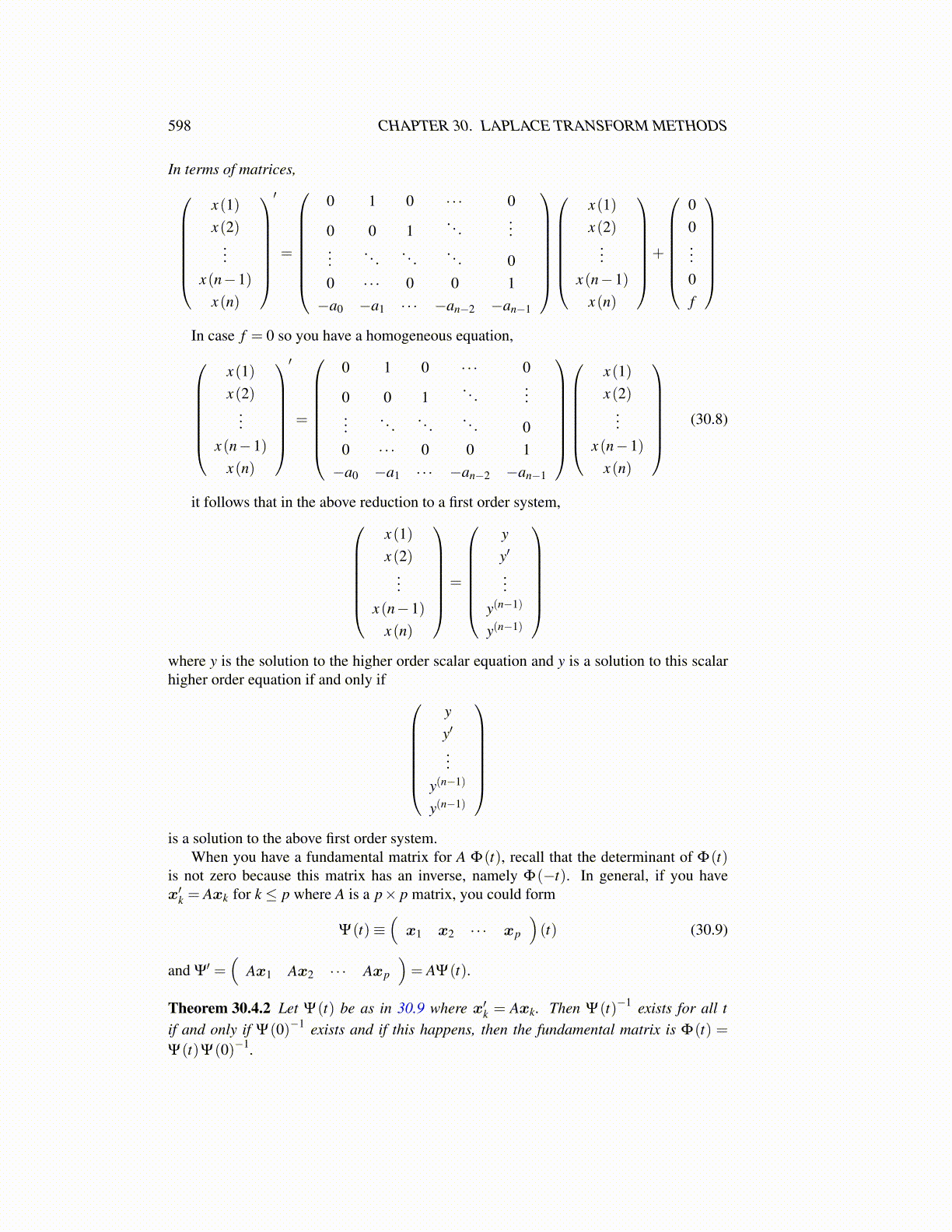
In terms of matrices,

x(1)x(2)

...x(n−1)

x(n)



′

=



0 1 0 · · · 0

0 0 1. . .

......

. . .. . .

. . . 00 · · · 0 0 1−a0 −a1 · · · −an−2 −an−1





x(1)x(2)

...x(n−1)

x(n)

+



00...0f

In case f = 0 so you have a homogeneous equation,

x(1)x(2)

...x(n−1)

x(n)



′

=



0 1 0 · · · 0

0 0 1. . .

......

. . . . . . . . . 00 · · · 0 0 1−a0 −a1 · · · −an−2 −an−1





x(1)x(2)

...x(n−1)

x(n)

 (30.8)

it follows that in the above reduction to a first order system,

x(1)x(2)

...x(n−1)

x(n)

=



yy′

...y(n−1)

y(n−1)

where y is the solution to the higher order scalar equation and y is a solution to this scalarhigher order equation if and only if 

yy′

...y(n−1)

y(n−1)

is a solution to the above first order system.

When you have a fundamental matrix for A Φ(t), recall that the determinant of Φ(t)is not zero because this matrix has an inverse, namely Φ(−t). In general, if you havex′k = Axk for k ≤ p where A is a p× p matrix, you could form

Ψ(t)≡(

x1 x2 · · · xp

)(t) (30.9)

and Ψ′ =(

Ax1 Ax2 · · · Axp

)= AΨ(t).

Theorem 30.4.2 Let Ψ(t) be as in 30.9 where x′k = Axk. Then Ψ(t)−1 exists for all tif and only if Ψ(0)−1 exists and if this happens, then the fundamental matrix is Φ(t) =Ψ(t)Ψ(0)−1.