32.6. THE BESSEL EQUATIONS 627

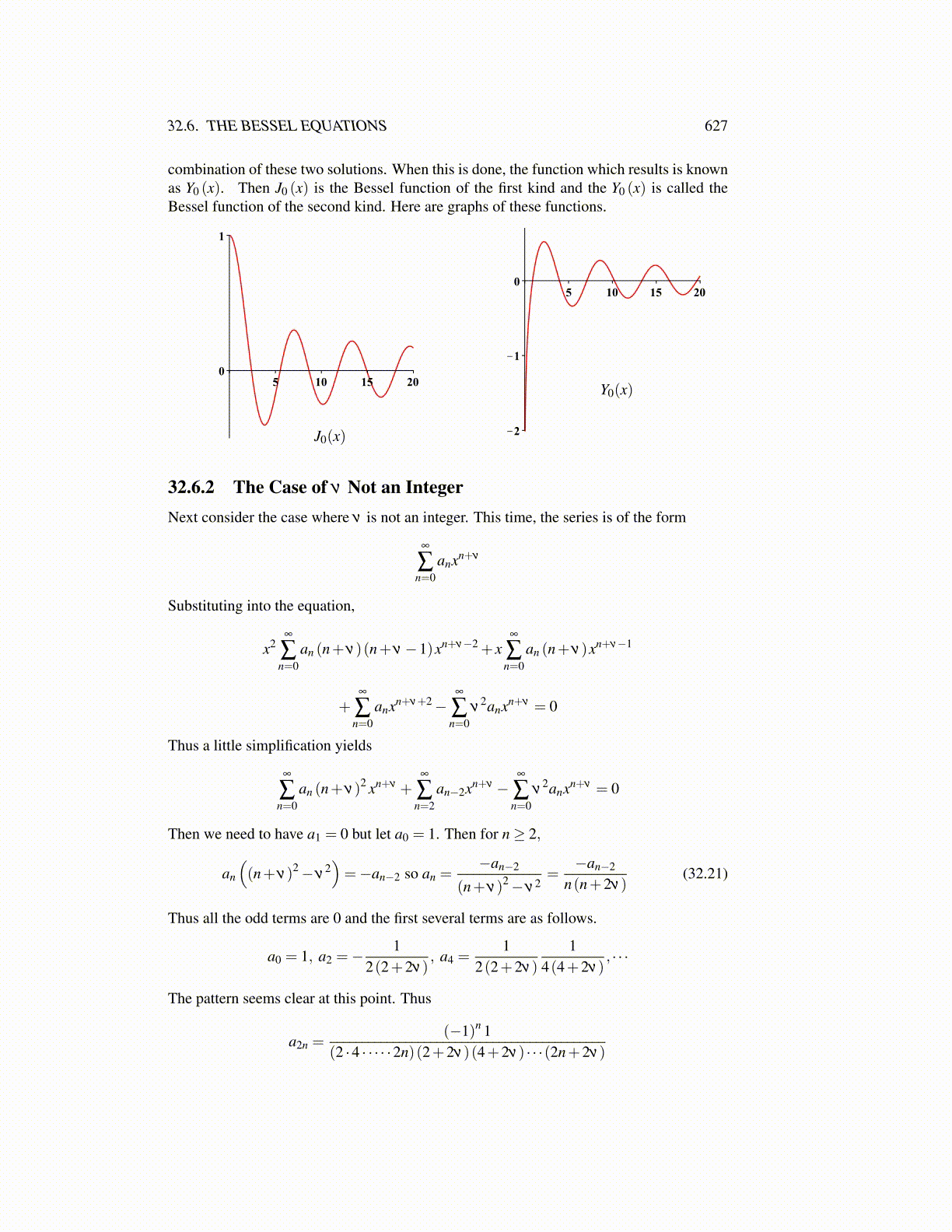
combination of these two solutions. When this is done, the function which results is knownas Y0 (x). Then J0 (x) is the Bessel function of the first kind and the Y0 (x) is called theBessel function of the second kind. Here are graphs of these functions.

J0(x)

Y0(x)

32.6.2 The Case of ν Not an IntegerNext consider the case where ν is not an integer. This time, the series is of the form

∞

∑n=0

anxn+ν

Substituting into the equation,

x2∞

∑n=0

an (n+ν)(n+ν−1)xn+ν−2 + x∞

∑n=0

an (n+ν)xn+ν−1

+∞

∑n=0

anxn+ν+2−∞

∑n=0

ν2anxn+ν = 0

Thus a little simplification yields

∞

∑n=0

an (n+ν)2 xn+ν +∞

∑n=2

an−2xn+ν −∞

∑n=0

ν2anxn+ν = 0

Then we need to have a1 = 0 but let a0 = 1. Then for n≥ 2,

an

((n+ν)2−ν

2)=−an−2 so an =

−an−2

(n+ν)2−ν2=−an−2

n(n+2ν)(32.21)

Thus all the odd terms are 0 and the first several terms are as follows.

a0 = 1, a2 =−1

2(2+2ν), a4 =

12(2+2ν)

14(4+2ν)

, · · ·

The pattern seems clear at this point. Thus

a2n =(−1)n 1

(2 ·4 · · · · ·2n)(2+2ν)(4+2ν) · · ·(2n+2ν)