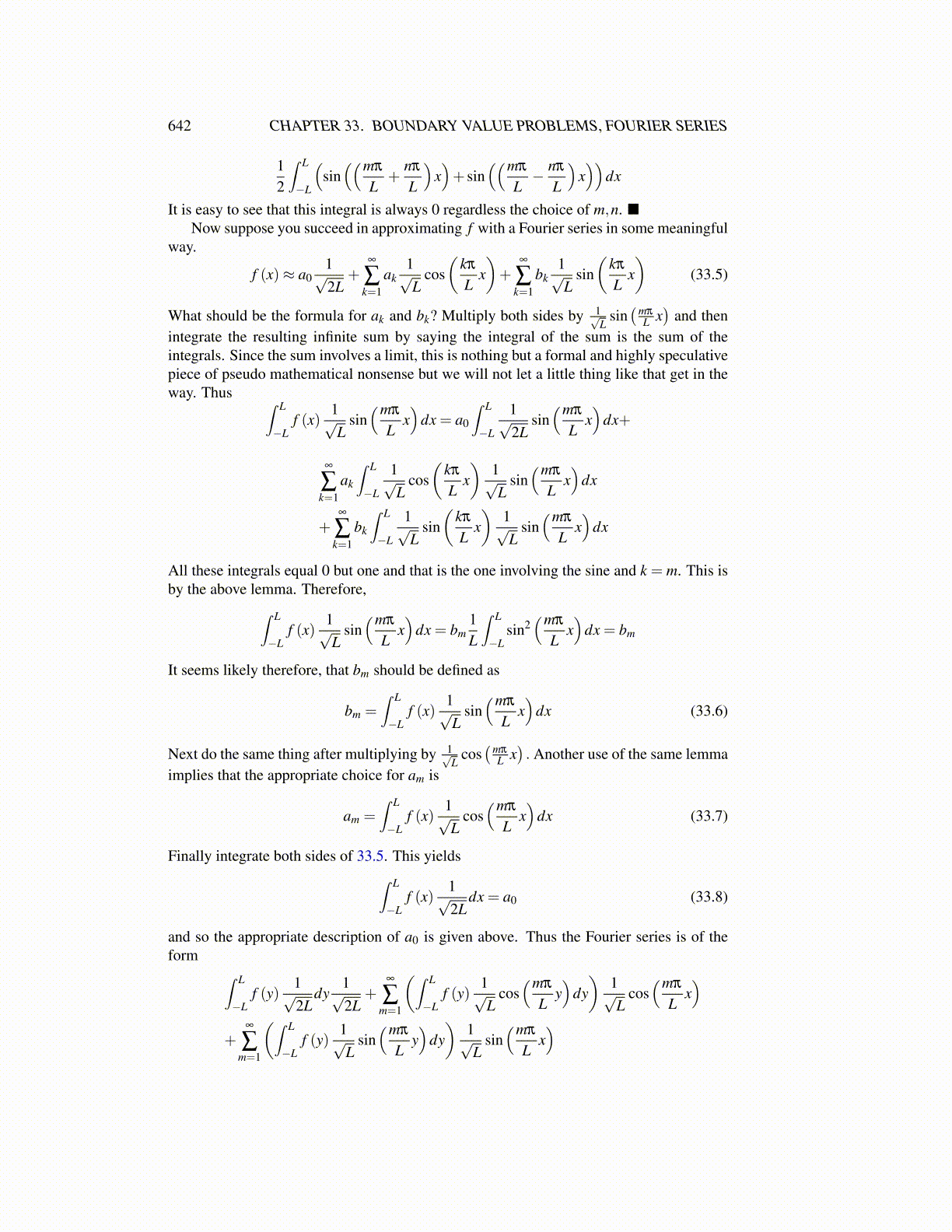
642 CHAPTER 33. BOUNDARY VALUE PROBLEMS, FOURIER SERIES

12

∫ L

−L

(sin((mπ

L+

nπ

L

)x)+ sin

((mπ

L− nπ

L

)x))

dx

It is easy to see that this integral is always 0 regardless the choice of m,n. ■Now suppose you succeed in approximating f with a Fourier series in some meaningful

way.

f (x)≈ a01√2L

+∞

∑k=1

ak1√L

cos(

kπ

Lx)+

∞

∑k=1

bk1√L

sin(

kπ

Lx)

(33.5)

What should be the formula for ak and bk? Multiply both sides by 1√L

sin(mπ

L x)

and thenintegrate the resulting infinite sum by saying the integral of the sum is the sum of theintegrals. Since the sum involves a limit, this is nothing but a formal and highly speculativepiece of pseudo mathematical nonsense but we will not let a little thing like that get in theway. Thus ∫ L

−Lf (x)

1√L

sin(mπ

Lx)

dx = a0

∫ L

−L

1√2L

sin(mπ

Lx)

dx+

∞

∑k=1

ak

∫ L

−L

1√L

cos(

kπ

Lx)

1√L

sin(mπ

Lx)

dx

+∞

∑k=1

bk

∫ L

−L

1√L

sin(

kπ

Lx)

1√L

sin(mπ

Lx)

dx

All these integrals equal 0 but one and that is the one involving the sine and k = m. This isby the above lemma. Therefore,∫ L

−Lf (x)

1√L

sin(mπ

Lx)

dx = bm1L

∫ L

−Lsin2

(mπ

Lx)

dx = bm

It seems likely therefore, that bm should be defined as

bm =∫ L

−Lf (x)

1√L

sin(mπ

Lx)

dx (33.6)

Next do the same thing after multiplying by 1√L

cos(mπ

L x). Another use of the same lemma

implies that the appropriate choice for am is

am =∫ L

−Lf (x)

1√L

cos(mπ

Lx)

dx (33.7)

Finally integrate both sides of 33.5. This yields∫ L

−Lf (x)

1√2L

dx = a0 (33.8)

and so the appropriate description of a0 is given above. Thus the Fourier series is of theform ∫ L

−Lf (y)

1√2L

dy1√2L

+∞

∑m=1

(∫ L

−Lf (y)

1√L

cos(mπ

Ly)

dy)

1√L

cos(mπ

Lx)

+∞

∑m=1

(∫ L

−Lf (y)

1√L

sin(mπ

Ly)

dy)

1√L

sin(mπ

Lx)