33.5. POINTWISE CONVERGENCE OF FOURIER SERIES 651

-2 0 20

1

2

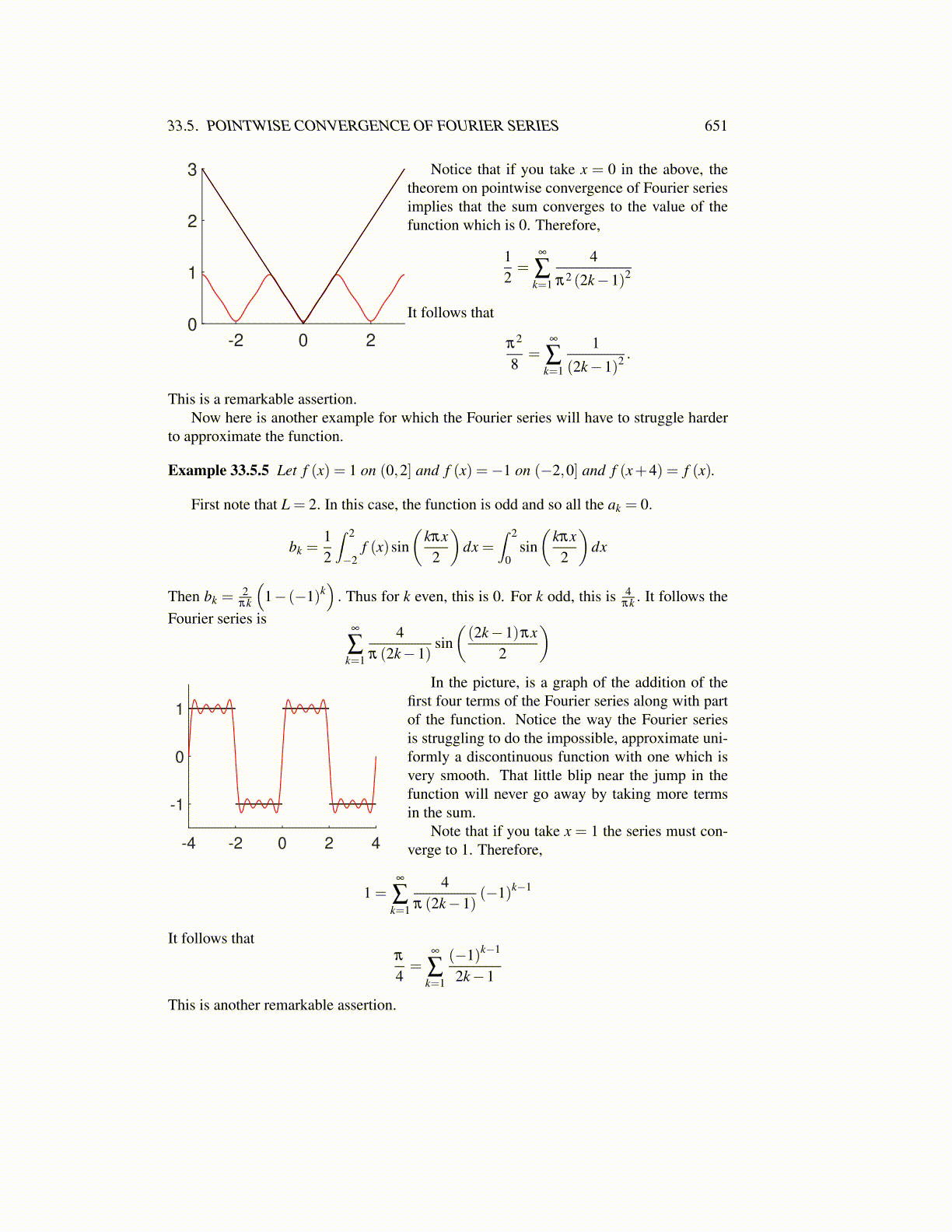
3 Notice that if you take x = 0 in the above, thetheorem on pointwise convergence of Fourier seriesimplies that the sum converges to the value of thefunction which is 0. Therefore,

12=

∞

∑k=1

4

π2 (2k−1)2

It follows that

π2

8=

∞

∑k=1

1

(2k−1)2 .

This is a remarkable assertion.Now here is another example for which the Fourier series will have to struggle harder

to approximate the function.

Example 33.5.5 Let f (x) = 1 on (0,2] and f (x) =−1 on (−2,0] and f (x+4) = f (x).

First note that L = 2. In this case, the function is odd and so all the ak = 0.

bk =12

∫ 2

−2f (x)sin

(kπx

2

)dx =

∫ 2

0sin(

kπx2

)dx

Then bk =2

πk

(1− (−1)k

). Thus for k even, this is 0. For k odd, this is 4

πk . It follows theFourier series is

∞

∑k=1

4π (2k−1)

sin((2k−1)πx

2

)

-4 -2 0 2 4

-1

0

1

In the picture, is a graph of the addition of thefirst four terms of the Fourier series along with partof the function. Notice the way the Fourier seriesis struggling to do the impossible, approximate uni-formly a discontinuous function with one which isvery smooth. That little blip near the jump in thefunction will never go away by taking more termsin the sum.

Note that if you take x = 1 the series must con-verge to 1. Therefore,

1 =∞

∑k=1

4π (2k−1)

(−1)k−1

It follows thatπ

4=

∞

∑k=1

(−1)k−1

2k−1

This is another remarkable assertion.