34.2. HEAT AND WAVE EQUATIONS 675

Then the solution to this problem is

∞

∑n=1

(32

π3 (2n−1)3 (2(−1)nπn− (−1)n

π +4)

)e−

110

((2n−1)π

4

)2t sin

((2n−1)πx

4

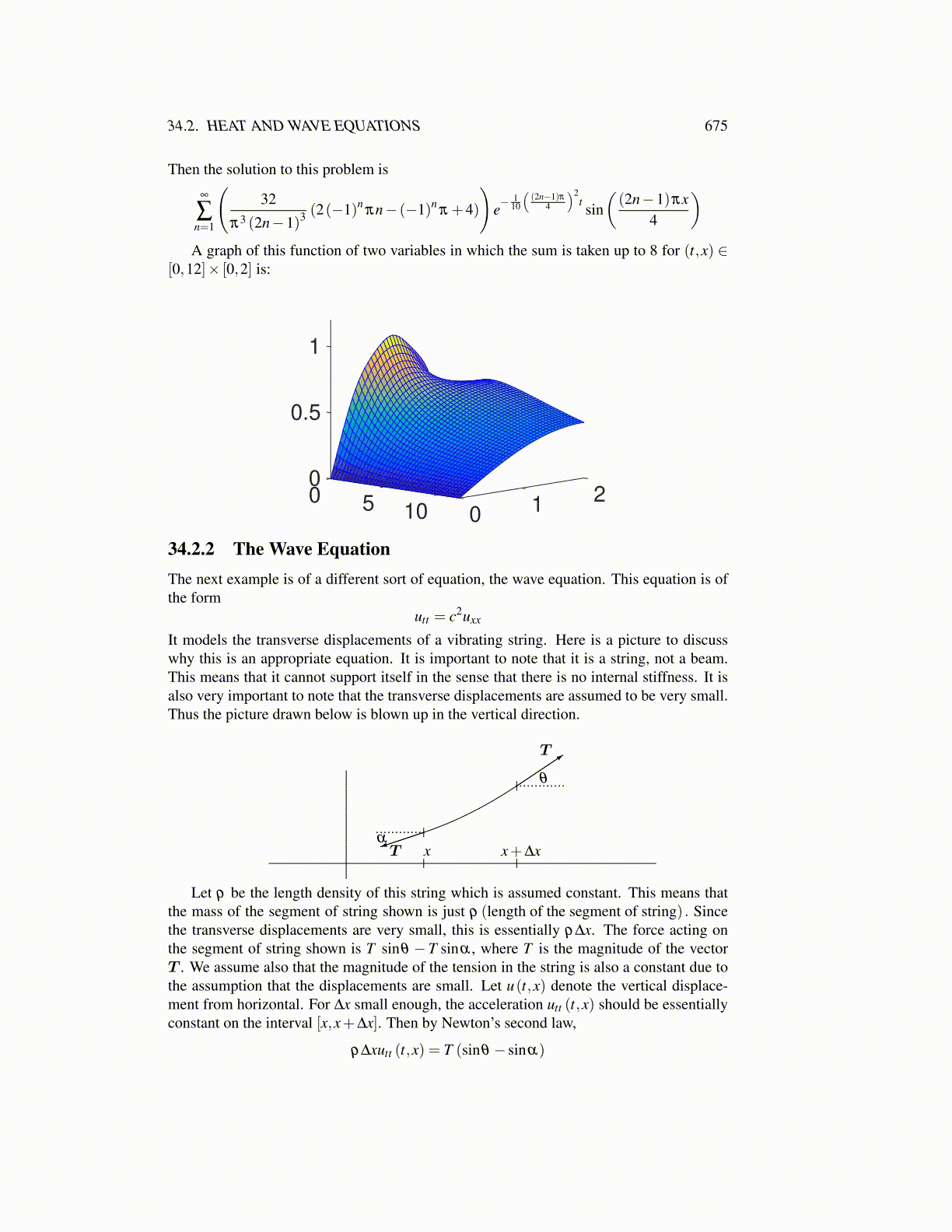
)A graph of this function of two variables in which the sum is taken up to 8 for (t,x) ∈

[0,12]× [0,2] is:

0

0.5

20

1

5 110 0

34.2.2 The Wave EquationThe next example is of a different sort of equation, the wave equation. This equation is ofthe form

utt = c2uxx

It models the transverse displacements of a vibrating string. Here is a picture to discusswhy this is an appropriate equation. It is important to note that it is a string, not a beam.This means that it cannot support itself in the sense that there is no internal stiffness. It isalso very important to note that the transverse displacements are assumed to be very small.Thus the picture drawn below is blown up in the vertical direction.

θ

T

αT x x+∆x

Let ρ be the length density of this string which is assumed constant. This means thatthe mass of the segment of string shown is just ρ (length of the segment of string) . Sincethe transverse displacements are very small, this is essentially ρ∆x. The force acting onthe segment of string shown is T sinθ −T sinα , where T is the magnitude of the vectorT . We assume also that the magnitude of the tension in the string is also a constant due tothe assumption that the displacements are small. Let u(t,x) denote the vertical displace-ment from horizontal. For ∆x small enough, the acceleration utt (t,x) should be essentiallyconstant on the interval [x,x+∆x]. Then by Newton’s second law,

ρ∆xutt (t,x) = T (sinθ − sinα)