112 CHAPTER 4. ROW OPERATIONS
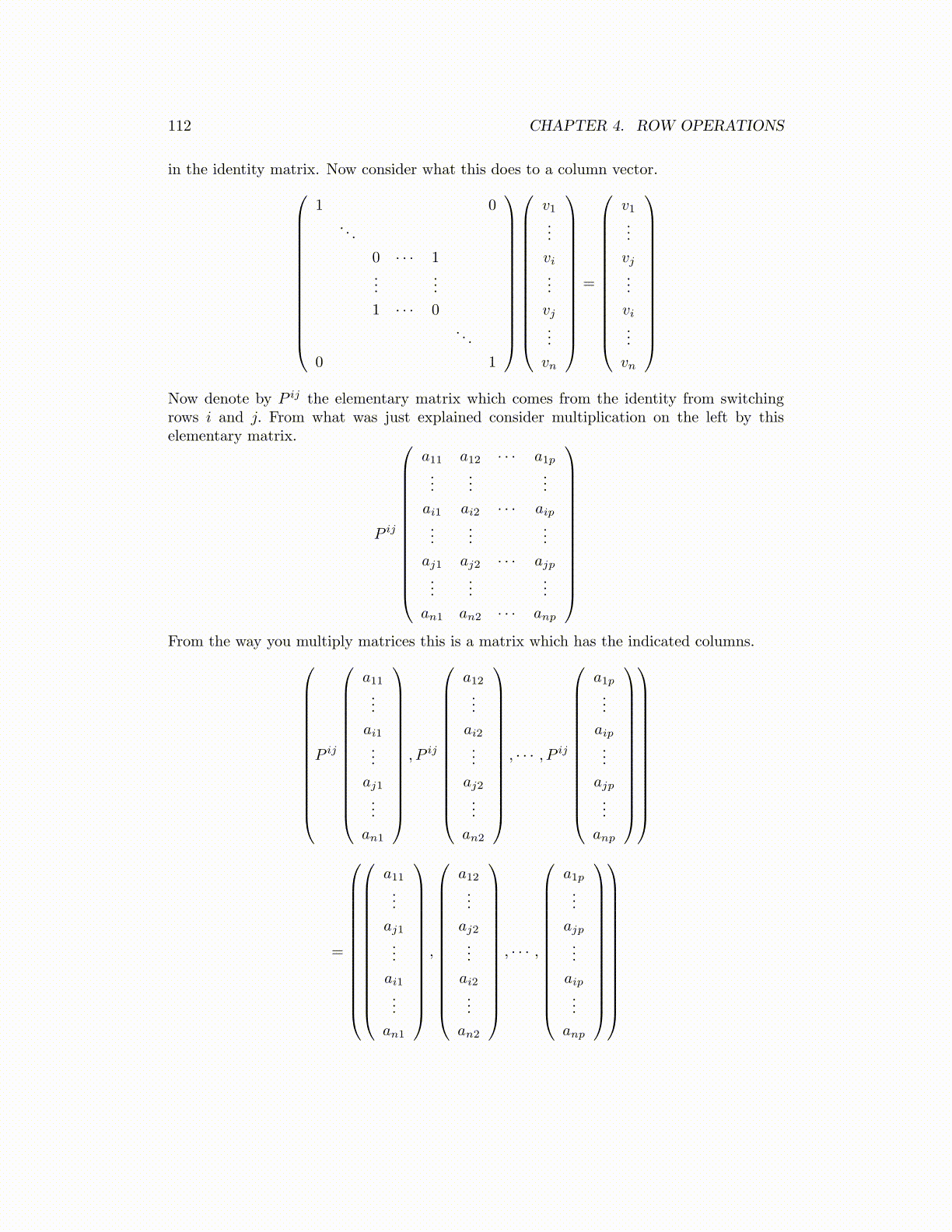
in the identity matrix. Now consider what this does to a column vector.
1 0. . .
0 · · · 1...
...
1 · · · 0. . .
0 1
v1...
vi...
vj...
vn
=
v1...
vj...
vi...
vn
Now denote by P ij the elementary matrix which comes from the identity from switchingrows i and j. From what was just explained consider multiplication on the left by thiselementary matrix.
P ij
a11 a12 · · · a1p...
......
ai1 ai2 · · · aip...
......
aj1 aj2 · · · ajp...
......
an1 an2 · · · anp
From the way you multiply matrices this is a matrix which has the indicated columns.
P ij
a11...
ai1...
aj1...
an1
, P ij
a12...
ai2...
aj2...
an2
, · · · , P ij
a1p...
aip...
ajp...
anp
=
a11...
aj1...
ai1...
an1
,
a12...
aj2...
ai2...
an2
, · · · ,
a1p...
ajp...
aip...
anp