248 CHAPTER 9. CANONICAL FORMS
be the same. Therefore, they comprise the same set of positive integers. Thus listing theeigenvalues in the same order, corresponding blocks J (λk) , J
′ (λk) are the same size.It remains to show that J (λk) and J ′ (λk) are not just the same size but also are the
same up to order of the Jordan blocks running down their respective diagonals. It is onlynecessary to worry about the number and size of the Jordan blocks making up J (λk) andJ ′ (λk) . Since J, J
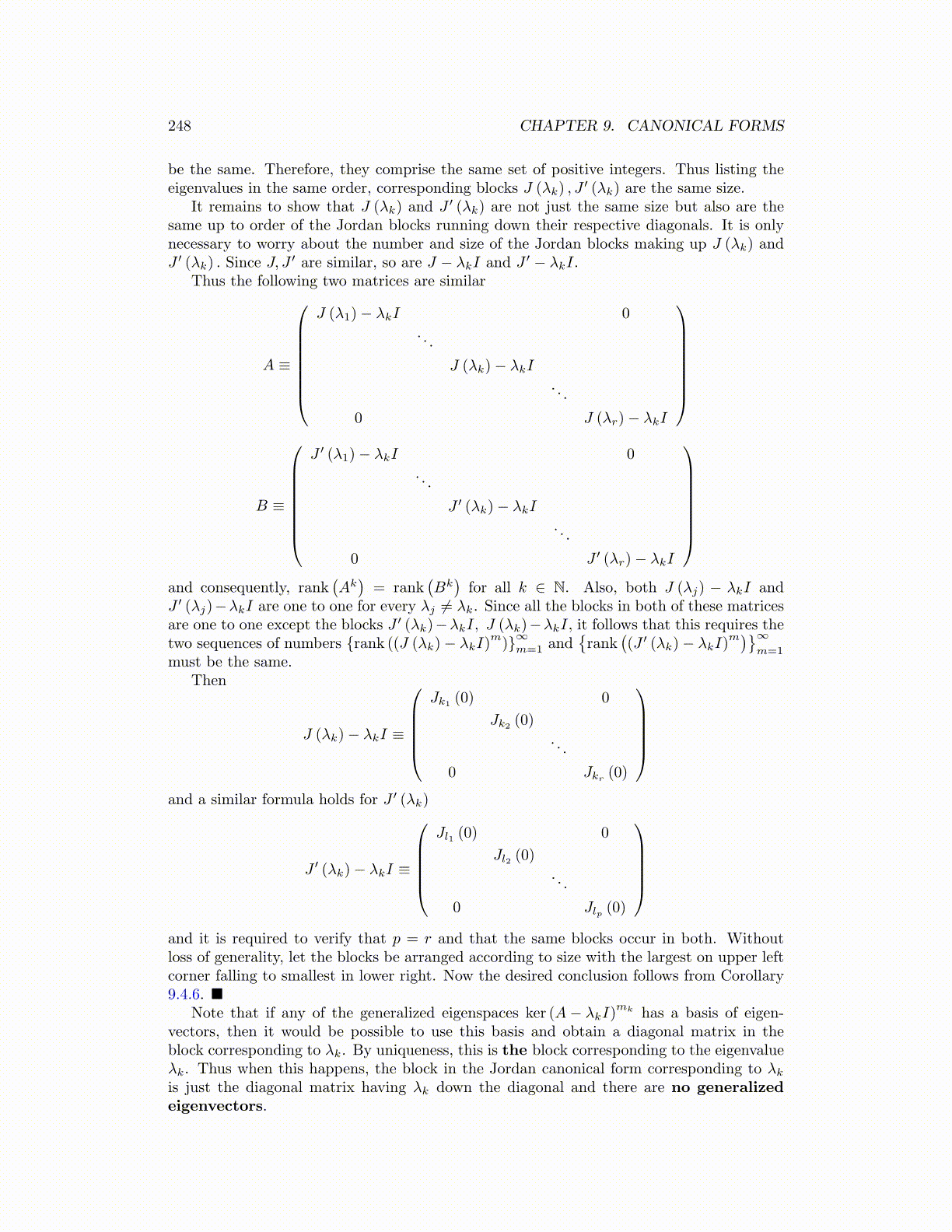
′ are similar, so are J − λkI and J ′ − λkI.Thus the following two matrices are similar
A ≡
J (λ1)− λkI 0. . .
J (λk)− λkI. . .
0 J (λr)− λkI
B ≡
J ′ (λ1)− λkI 0. . .
J ′ (λk)− λkI. . .
0 J ′ (λr)− λkI
and consequently, rank
(Ak)= rank
(Bk)for all k ∈ N. Also, both J (λj) − λkI and
J ′ (λj)−λkI are one to one for every λj ̸= λk. Since all the blocks in both of these matricesare one to one except the blocks J ′ (λk)−λkI, J (λk)−λkI, it follows that this requires thetwo sequences of numbers {rank ((J (λk)− λkI)
m)}∞m=1 and
{rank
((J ′ (λk)− λkI)
m)}∞m=1
must be the same.Then
J (λk)− λkI ≡
Jk1 (0) 0
Jk2 (0). . .
0 Jkr(0)
and a similar formula holds for J ′ (λk)
J ′ (λk)− λkI ≡
Jl1 (0) 0
Jl2 (0). . .
0 Jlp (0)
and it is required to verify that p = r and that the same blocks occur in both. Withoutloss of generality, let the blocks be arranged according to size with the largest on upper leftcorner falling to smallest in lower right. Now the desired conclusion follows from Corollary9.4.6. ■
Note that if any of the generalized eigenspaces ker (A− λkI)mk has a basis of eigen-
vectors, then it would be possible to use this basis and obtain a diagonal matrix in theblock corresponding to λk. By uniqueness, this is the block corresponding to the eigenvalueλk. Thus when this happens, the block in the Jordan canonical form corresponding to λkis just the diagonal matrix having λk down the diagonal and there are no generalizedeigenvectors.