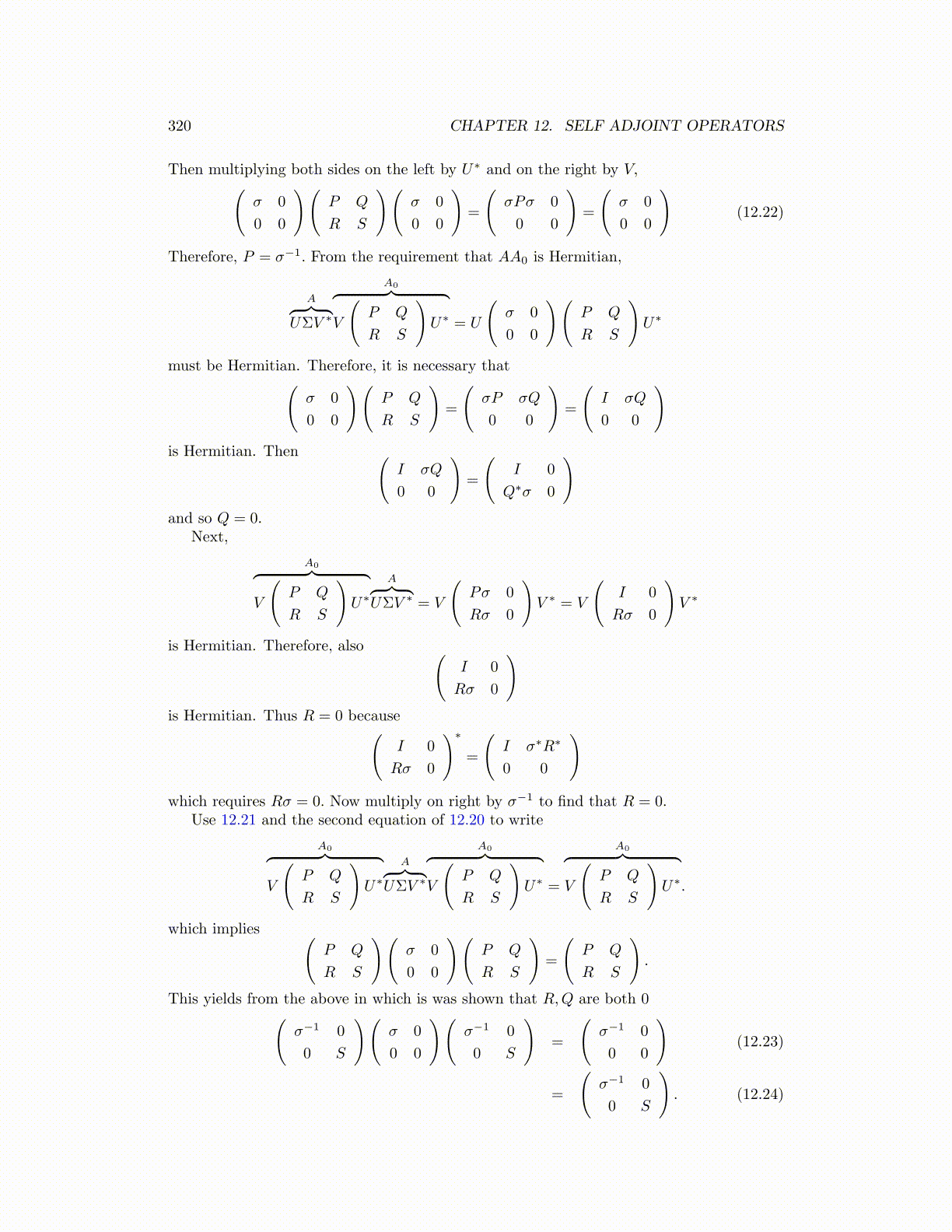
320 CHAPTER 12. SELF ADJOINT OPERATORS
Then multiplying both sides on the left by U∗ and on the right by V,(σ 0
0 0
)(P Q
R S
)(σ 0
0 0
)=
(σPσ 0
0 0
)=
(σ 0
0 0
)(12.22)
Therefore, P = σ−1. From the requirement that AA0 is Hermitian,
A︷ ︸︸ ︷UΣV ∗
A0︷ ︸︸ ︷V
(P Q
R S
)U∗ = U
(σ 0
0 0
)(P Q
R S
)U∗
must be Hermitian. Therefore, it is necessary that(σ 0
0 0
)(P Q
R S
)=
(σP σQ
0 0
)=
(I σQ
0 0
)is Hermitian. Then (
I σQ
0 0
)=
(I 0
Q∗σ 0
)and so Q = 0.
Next,
A0︷ ︸︸ ︷V
(P Q
R S
)U∗
A︷ ︸︸ ︷UΣV ∗ = V
(Pσ 0
Rσ 0
)V ∗ = V
(I 0
Rσ 0
)V ∗
is Hermitian. Therefore, also (I 0
Rσ 0
)is Hermitian. Thus R = 0 because(
I 0
Rσ 0
)∗
=
(I σ∗R∗
0 0
)which requires Rσ = 0. Now multiply on right by σ−1 to find that R = 0.
Use 12.21 and the second equation of 12.20 to write
A0︷ ︸︸ ︷V
(P Q
R S
)U∗
A︷ ︸︸ ︷UΣV ∗
A0︷ ︸︸ ︷V
(P Q
R S
)U∗ =
A0︷ ︸︸ ︷V
(P Q
R S
)U∗.
which implies (P Q
R S
)(σ 0
0 0
)(P Q
R S
)=
(P Q
R S
).
This yields from the above in which is was shown that R,Q are both 0(σ−1 0
0 S
)(σ 0
0 0
)(σ−1 0
0 S
)=
(σ−1 0
0 0
)(12.23)
=
(σ−1 0
0 S
). (12.24)