2.1. MATRICES 39
All the above is fine, but the real reason for considering matrices is that they can bemultiplied. This is where things quit being banal.
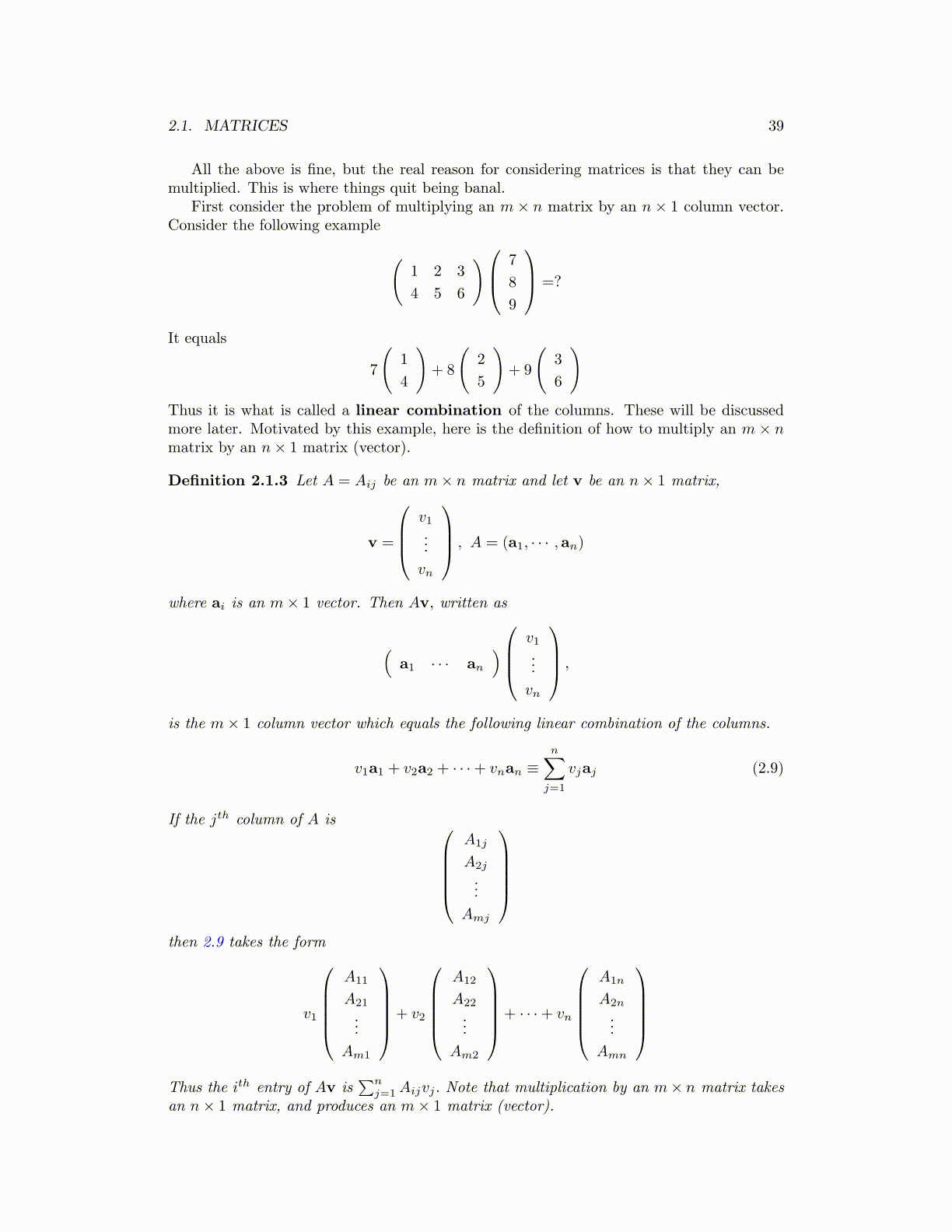
First consider the problem of multiplying an m × n matrix by an n × 1 column vector.Consider the following example
(1 2 3
4 5 6
) 7
8
9
=?
It equals
7
(1
4
)+ 8
(2
5
)+ 9
(3
6
)Thus it is what is called a linear combination of the columns. These will be discussedmore later. Motivated by this example, here is the definition of how to multiply an m × nmatrix by an n× 1 matrix (vector).
Definition 2.1.3 Let A = Aij be an m× n matrix and let v be an n× 1 matrix,
v =
v1...
vn
, A = (a1, · · · ,an)
where ai is an m× 1 vector. Then Av, written as
(a1 · · · an
)v1...
vn
,
is the m× 1 column vector which equals the following linear combination of the columns.
v1a1 + v2a2 + · · ·+ vnan ≡n∑
j=1
vjaj (2.9)
If the jth column of A is A1j
A2j
...
Amj
then 2.9 takes the form
v1
A11
A21
...
Am1
+ v2
A12
A22
...
Am2
+ · · ·+ vn
A1n
A2n
...
Amn
Thus the ith entry of Av is
∑nj=1Aijvj . Note that multiplication by an m× n matrix takes
an n× 1 matrix, and produces an m× 1 matrix (vector).