398 APPENDIX C. FUNCTIONS OF MATRICES
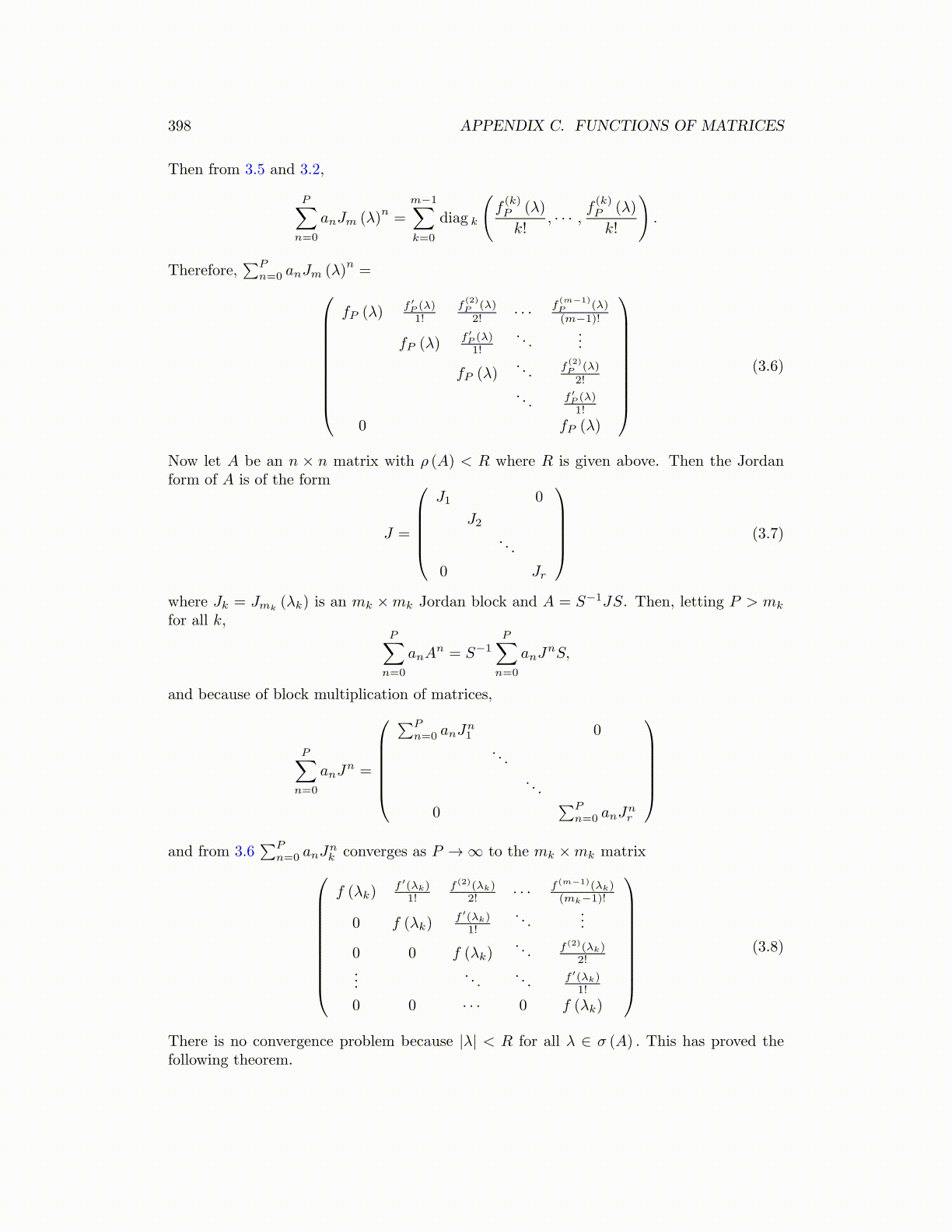
Then from 3.5 and 3.2,
P∑n=0
anJm (λ)n=
m−1∑k=0
diag k
(f(k)P (λ)
k!, · · · ,
f(k)P (λ)
k!
).
Therefore,∑P
n=0 anJm (λ)n=
fP (λ)f ′P (λ)1!
f(2)P (λ)
2! · · · f(m−1)P (λ)
(m−1)!
fP (λ)f ′P (λ)1!
. . ....
fP (λ). . . f
(2)P (λ)
2!
. . . f ′P (λ)1!
0 fP (λ)
(3.6)
Now let A be an n × n matrix with ρ (A) < R where R is given above. Then the Jordanform of A is of the form
J =
J1 0
J2. . .
0 Jr
(3.7)
where Jk = Jmk(λk) is an mk ×mk Jordan block and A = S−1JS. Then, letting P > mk
for all k,P∑
n=0
anAn = S−1
P∑n=0
anJnS,
and because of block multiplication of matrices,
P∑n=0
anJn =
∑P
n=0 anJn1 0
. . .
. . .
0∑P
n=0 anJnr
and from 3.6
∑Pn=0 anJ
nk converges as P → ∞ to the mk ×mk matrix
f (λk)f ′(λk)
1!f(2)(λk)
2! · · · f(m−1)(λk)(mk−1)!
0 f (λk)f ′(λk)
1!
. . ....
0 0 f (λk). . . f(2)(λk)
2!...
. . .. . . f ′(λk)
1!
0 0 · · · 0 f (λk)
(3.8)
There is no convergence problem because |λ| < R for all λ ∈ σ (A) . This has proved thefollowing theorem.