44 CHAPTER 2. LINEAR TRANSFORMATIONS

2.1.2 Digraphs

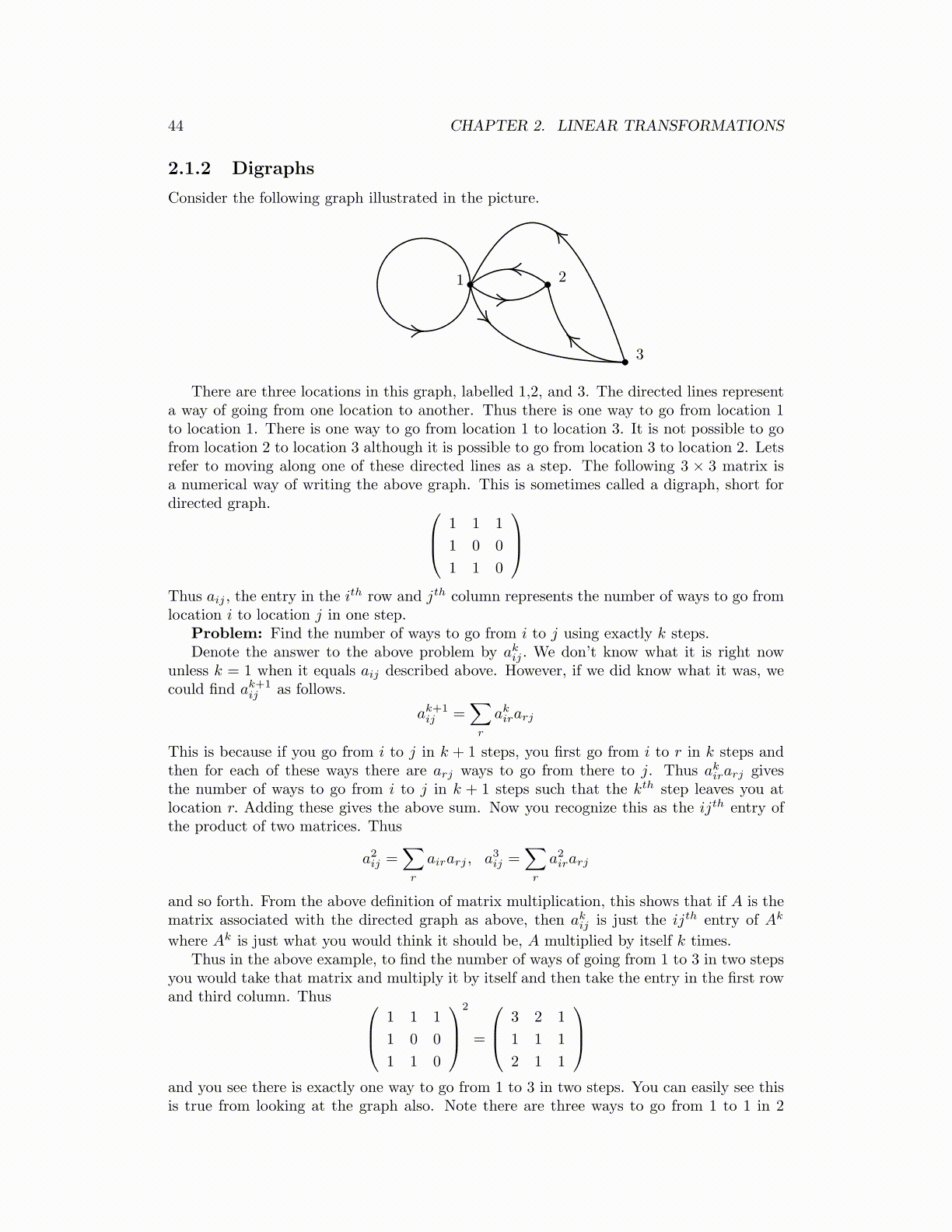
Consider the following graph illustrated in the picture.

1 2

3

There are three locations in this graph, labelled 1,2, and 3. The directed lines representa way of going from one location to another. Thus there is one way to go from location 1to location 1. There is one way to go from location 1 to location 3. It is not possible to gofrom location 2 to location 3 although it is possible to go from location 3 to location 2. Letsrefer to moving along one of these directed lines as a step. The following 3 × 3 matrix isa numerical way of writing the above graph. This is sometimes called a digraph, short fordirected graph.  1 1 1

1 0 0

1 1 0

Thus aij , the entry in the ith row and jth column represents the number of ways to go fromlocation i to location j in one step.

Problem: Find the number of ways to go from i to j using exactly k steps.Denote the answer to the above problem by akij . We don’t know what it is right now

unless k = 1 when it equals aij described above. However, if we did know what it was, wecould find ak+1

ij as follows.

ak+1ij =

∑r

akirarj

This is because if you go from i to j in k + 1 steps, you first go from i to r in k steps andthen for each of these ways there are arj ways to go from there to j. Thus akirarj givesthe number of ways to go from i to j in k + 1 steps such that the kth step leaves you atlocation r. Adding these gives the above sum. Now you recognize this as the ijth entry ofthe product of two matrices. Thus

a2ij =∑r

airarj , a3ij =∑r

a2irarj

and so forth. From the above definition of matrix multiplication, this shows that if A is thematrix associated with the directed graph as above, then akij is just the ijth entry of Ak

where Ak is just what you would think it should be, A multiplied by itself k times.Thus in the above example, to find the number of ways of going from 1 to 3 in two steps

you would take that matrix and multiply it by itself and then take the entry in the first rowand third column. Thus  1 1 1

1 0 0

1 1 0

2

=

 3 2 1

1 1 1

2 1 1

and you see there is exactly one way to go from 1 to 3 in two steps. You can easily see thisis true from looking at the graph also. Note there are three ways to go from 1 to 1 in 2