90 CHAPTER 3. DETERMINANTS
Proof: Define sign (x) = 1 if x > 0,−1 if x < 0 and 0 if x = 0. If n = 1, there is onlyone list and it is just the number 1. Thus one can define sgn1 (1) ≡ 1. For the general casewhere n > 1, simply define
sgnn (i1, · · · , in) ≡ sign
(∏r<s
(is − ir)
)
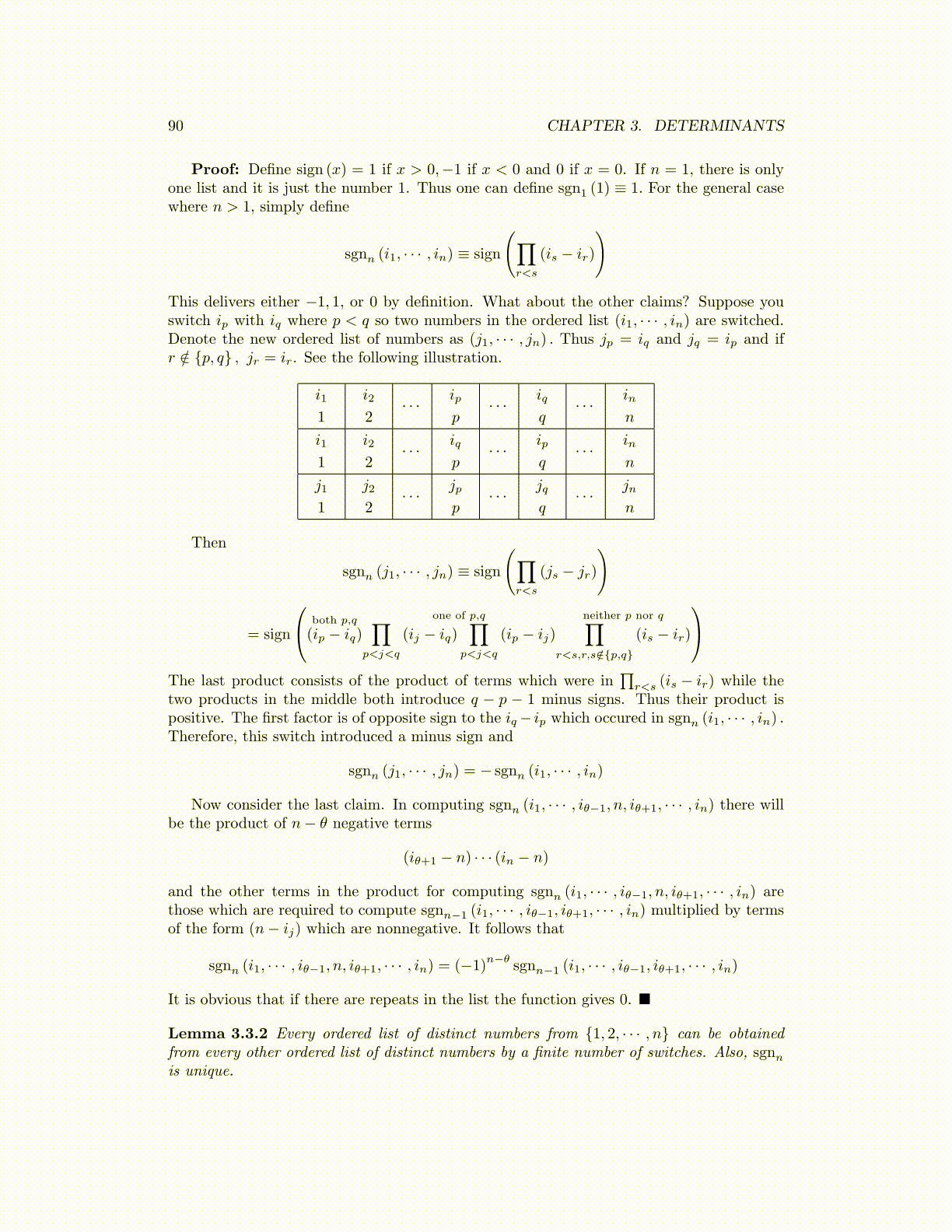
This delivers either −1, 1, or 0 by definition. What about the other claims? Suppose youswitch ip with iq where p < q so two numbers in the ordered list (i1, · · · , in) are switched.Denote the new ordered list of numbers as (j1, · · · , jn) . Thus jp = iq and jq = ip and ifr /∈ {p, q} , jr = ir. See the following illustration.
i1
1
i2
2· · · ip
p· · · iq
q· · · in
n
i1
1
i2
2· · · iq
p· · · ip
q· · · in
n
j1
1
j2
2· · · jp
p· · · jq
q· · · jn
n
Then
sgnn (j1, · · · , jn) ≡ sign
(∏r<s
(js − jr)
)
= sign
both p,q
(ip − iq)
one of p,q∏p<j<q
(ij − iq)∏
p<j<q
(ip − ij)
neither p nor q∏r<s,r,s/∈{p,q}
(is − ir)
The last product consists of the product of terms which were in
∏r<s (is − ir) while the
two products in the middle both introduce q − p − 1 minus signs. Thus their product ispositive. The first factor is of opposite sign to the iq− ip which occured in sgnn (i1, · · · , in) .Therefore, this switch introduced a minus sign and
sgnn (j1, · · · , jn) = − sgnn (i1, · · · , in)
Now consider the last claim. In computing sgnn (i1, · · · , iθ−1, n, iθ+1, · · · , in) there willbe the product of n− θ negative terms
(iθ+1 − n) · · · (in − n)
and the other terms in the product for computing sgnn (i1, · · · , iθ−1, n, iθ+1, · · · , in) arethose which are required to compute sgnn−1 (i1, · · · , iθ−1, iθ+1, · · · , in) multiplied by termsof the form (n− ij) which are nonnegative. It follows that
sgnn (i1, · · · , iθ−1, n, iθ+1, · · · , in) = (−1)n−θ
sgnn−1 (i1, · · · , iθ−1, iθ+1, · · · , in)
It is obvious that if there are repeats in the list the function gives 0. ■
Lemma 3.3.2 Every ordered list of distinct numbers from {1, 2, · · · , n} can be obtainedfrom every other ordered list of distinct numbers by a finite number of switches. Also, sgnnis unique.