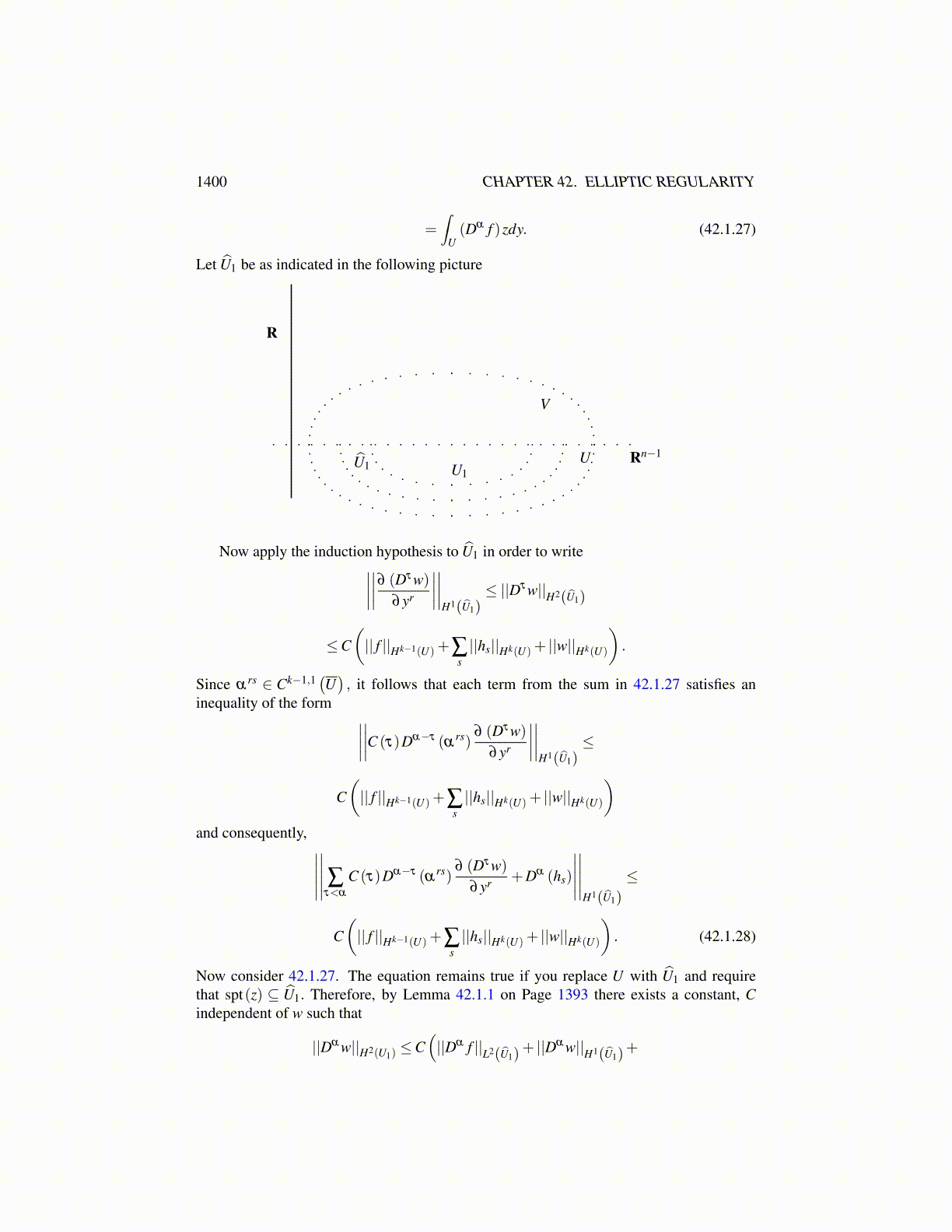
1400 CHAPTER 42. MAXIMAL MONOTONE OPERATORS, HILBERT SPACE
Theorem 42.6.1 Let A and B be maximal monotone operators and let xλ be the solution to
y ∈ xλ +Bλ xλ +Axλ .
Then y ∈ x+Bx+Ax for some x ∈ D(A)∩D(B) if Bλ xλ is bounded independent of λ .
The following is the perturbation theorem of this section. See [24] and [116].
Theorem 42.6.2 Let H be a real Hilbert space and let Φ be non negative, convex, proper,and lower semicontinuous. Suppose also that A is a maximal monotone operator and thereexists
ξ ∈ D(A)∩D(Φ) . (42.6.40)
Suppose also that for Jλ x≡ (I +λA)−1 x,
Φ(Jλ x)≤Φ(x)+Cλ (42.6.41)
Then A+∂Φ is maximal monotone.
Proof: Letting Aλ be the Yosida approximation of A,
Aλ x =1λ(x− Jλ x) ,
and letting y ∈ H, it follows from the Hilbert space version of Proposition 42.1.6 thereexists xλ ∈ H such that
y ∈ xλ +Aλ xλ +∂Φ(xλ ) .
Consequently,y− xλ −Aλ xλ ∈ ∂Φ(xλ ) (42.6.42)
and so(y− xλ −Aλ xλ ,Jλ xλ − xλ )≤Φ(Jλ xλ )−Φ(xλ )≤Cλ (42.6.43)
which implies
−(y− xλ −Aλ xλ ,Aλ xλ ) = |Aλ xλ |2−|y− xλ | |Aλ xλ | ≤C. (42.6.44)
By 42.6.42 and monotonicity of Aλ ,
Φ(ξ )−Φ(xλ )≥
∈∂Φ(xλ )︷ ︸︸ ︷y− xλ −Aλ xλ ,ξ − xλ
= (y− xλ ,ξ − xλ )− (Aλ xλ ,ξ − xλ )
≥ (y− xλ ,ξ − xλ )− (Aλ ξ ,ξ − xλ )
≥ (y−ξ ,ξ − xλ )+ |ξ − xλ |2− (Aλ ξ ,ξ − xλ )
= |ξ − xλ |2 +(y−ξ −Aλ ξ ,ξ − xλ )