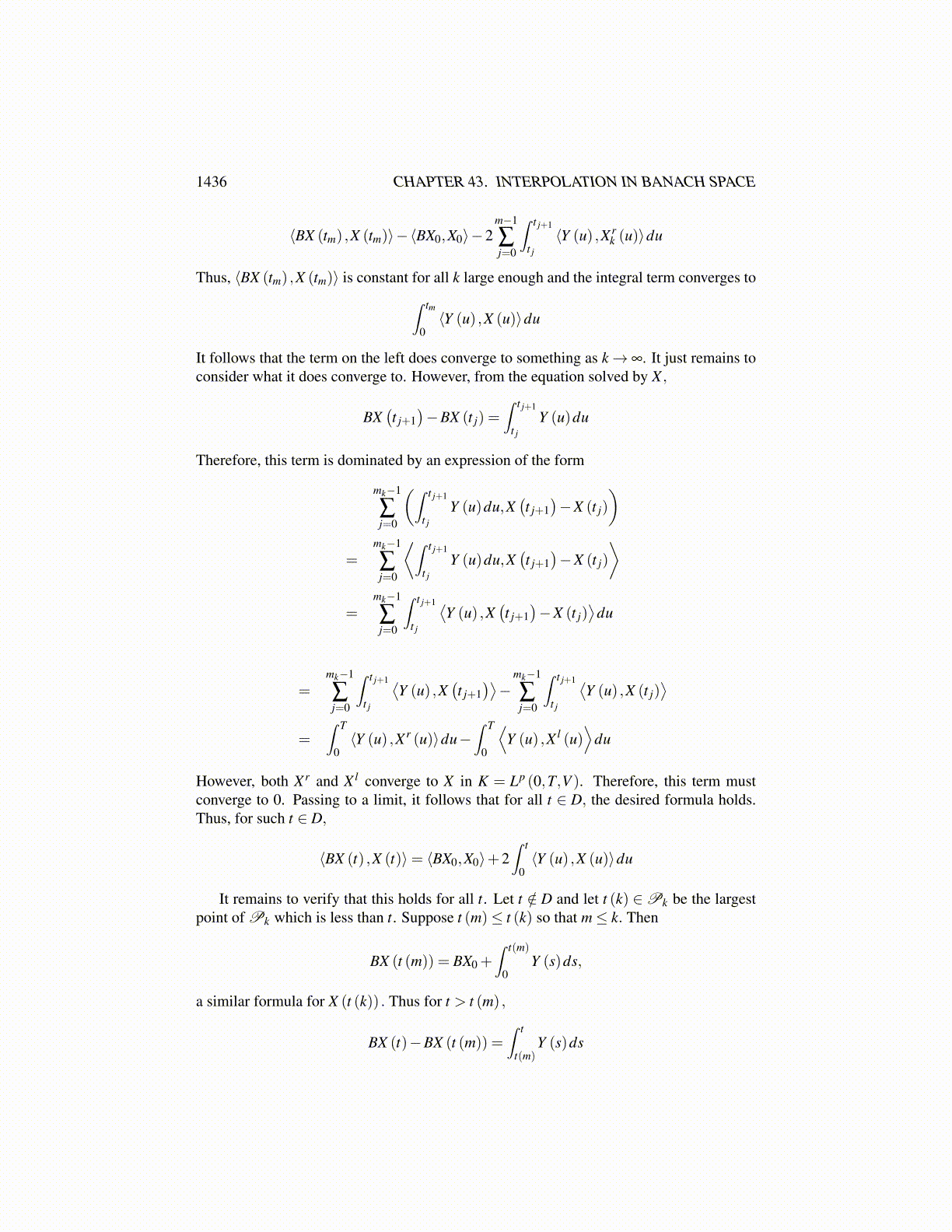
1436 CHAPTER 43. INTERPOLATION IN BANACH SPACE

Proof: It follows from the following computations

B(X (t)−X (s)) =∫ t

sY (u)du

and so

2∫ t

s⟨Y (u) ,X (t)⟩du−⟨B(X (t)−X (s)) ,(X (t)−X (s))⟩

= 2⟨B(X (t)−X (s)) ,X (t)⟩−⟨B(X (t)−X (s)) ,(X (t)−X (s))⟩

= 2⟨BX (t) ,X (t)⟩−2⟨BX (s) ,X (t)⟩−⟨BX (t) ,X (t)⟩+2⟨BX (s) ,X (t)⟩−⟨BX (s) ,X (s)⟩

= ⟨BX (t) ,X (t)⟩−⟨BX (s) ,X (s)⟩

Thus⟨BX (t) ,X (t)⟩−⟨BX (s) ,X (s)⟩

= 2∫ t

s⟨Y (u) ,X (t)⟩du−⟨B(X (t)−X (s)) ,(X (t)−X (s))⟩

Lemma 43.3.4 In the above situation,

supt∈[0,T ]

⟨BX (t) ,X (t)⟩ ≤C (∥Y∥K′ ,∥X∥K)

Also, t→ BX (t) is weakly continuous with values in W ′.

Proof: From the above formula applied to the kth partition of [0,T ] described above,

⟨BX (tm) ,X (tm)⟩−⟨BX0,X0⟩=m−1

∑j=0

⟨BX(t j+1

),X(t j+1

)⟩−⟨BX (t j) ,X (t j)

⟩

=m−1

∑j=0

2∫ t j+1

t j

⟨Y (u) ,X

(t j+1

)⟩du−

⟨B(X(t j+1

)−X (t j)

),X(t j+1

)−X (t j)

⟩=

m−1

∑j=0

2∫ t j+1

t j

⟨Y (u) ,X rk (u)⟩du−

⟨B(X(t j+1

)−X (t j)

),X(t j+1

)−X (t j)

⟩Thus, discarding the negative terms and denoting by Pk the kth of these partitions,

supt j∈Pk

⟨BX (t j) ,X (t j)

⟩≤ ⟨BX0,X0⟩+2

∫ T

0|⟨Y (u) ,X r

k (u)⟩|du

≤ ⟨BX0,X0⟩+2∫ T

0∥Y (u)∥V ′ ∥X

rk (u)∥V du