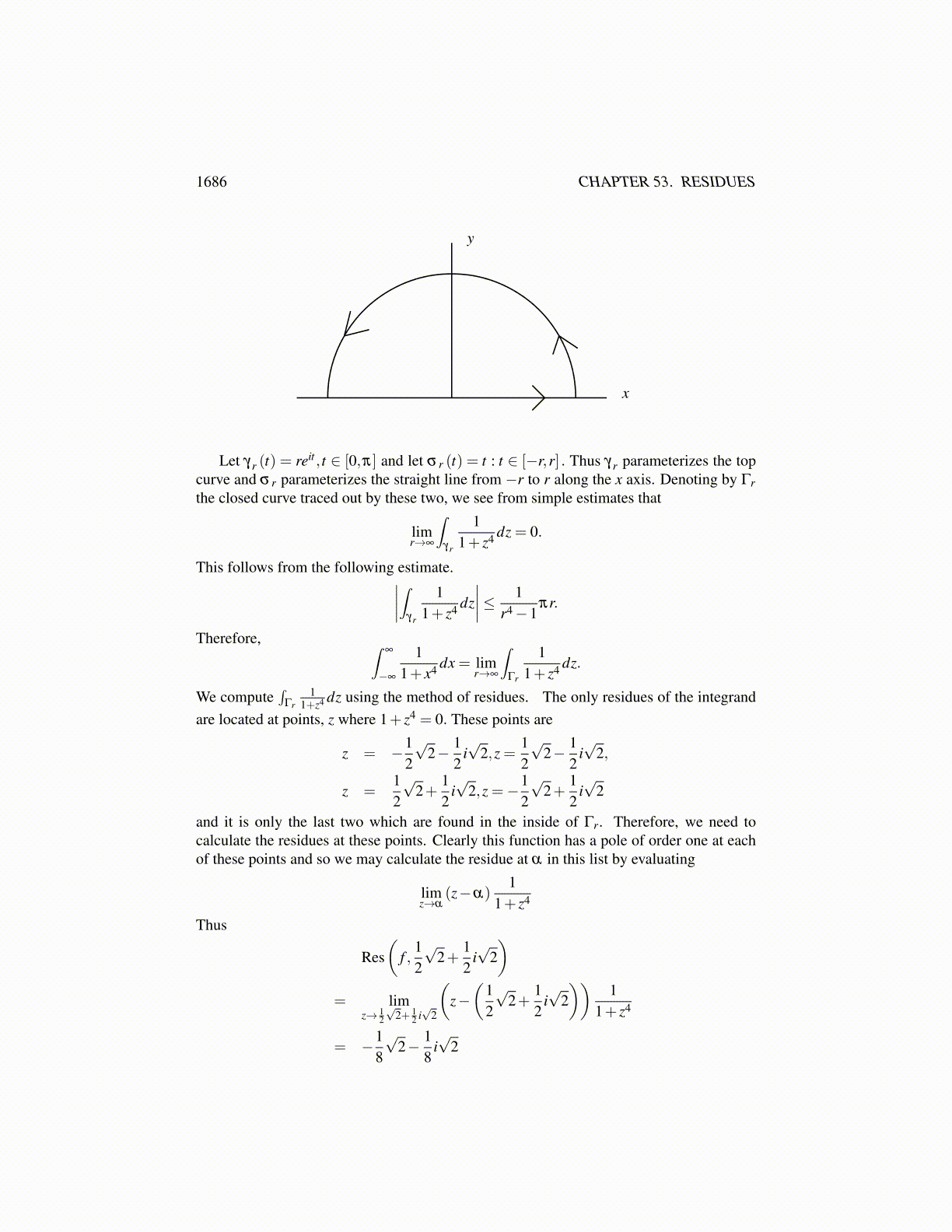
1686 CHAPTER 53. RESIDUES

Therefore, by Lemma 53.2.3, for any r ∈ (R1,R2) ,

f (z) =∞

∑n=0

(1

2πi

∫γr

f (w)

(w−a)n+1 dw

)(z−a)n+

−1

∑n=−∞

(1

2πi

∫γr

f (w)

(w−a)n+1

)(z−a)n . (53.2.9)

and so

f (z) =∞

∑n=−∞

(1

2πi

∫γr

f (w)

(w−a)n+1 dw

)(z−a)n .

where r ∈ (R1,R2) is arbitrary. This proves the existence part of the theorem. It remains tocharacterize an.

If f (z) = ∑∞n=−∞ an (z−a)n on ann(a,R1,R2) let

fn (z)≡n

∑k=−n

ak (z−a)k . (53.2.10)

This function is analytic in ann(a,R1,R2) and so from the above argument,

fn (z) =∞

∑k=−∞

(1

2πi

∫γr

fn (w)

(w−a)k+1 dw

)(z−a)k . (53.2.11)

Also if k > n or if k <−n, (1

2πi

∫γr

fn (w)

(w−a)k+1 dw

)= 0.

and so

fn (z) =n

∑k=−n

(1

2πi

∫γr

fn (w)

(w−a)k+1 dw

)(z−a)k

which implies from 53.2.10 that for each k ∈ [−n,n] ,

12πi

∫γr

fn (w)

(w−a)k+1 dw = ak

However, from the uniform convergence of the series,

∞

∑n=0

an (w−a)n

and∞

∑n=1

a−n (w−a)−n