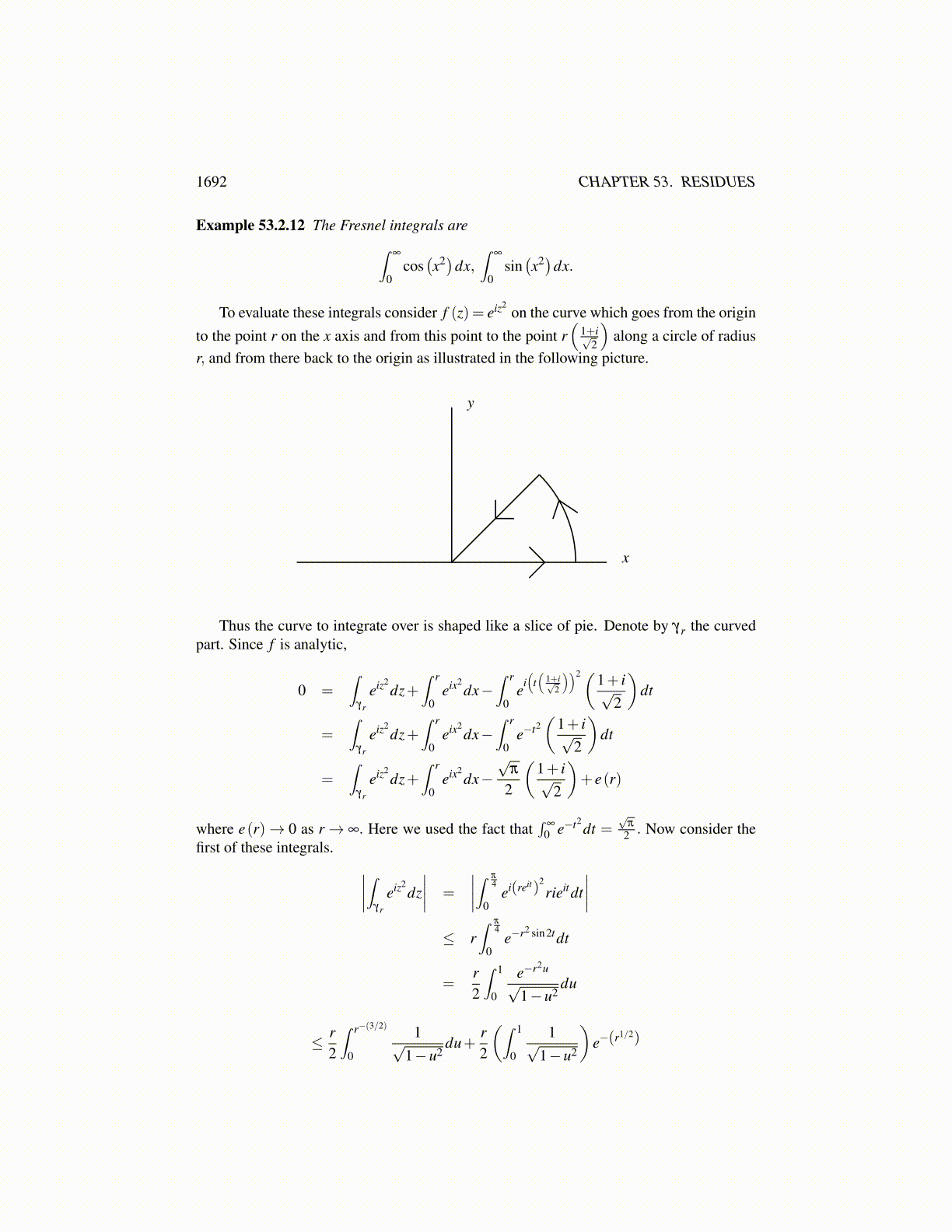
1692 CHAPTER 53. RESIDUES

for all |z| sufficiently small. It turns out there exists an explicit formula for this Mellintransformation under these conditions. Consider the following contour.

−R

In this contour the small semicircle in the center has radius ε which will converge to 0.Denote by γR the large circular path which starts at the upper edge of the slot and continuesto the lower edge. Denote by γε the small semicircular contour and denote by γεR+ thestraight part of the contour from 0 to R which provides the top edge of the slot. Finallydenote by γεR− the straight part of the contour from R to 0 which provides the bottom edgeof the slot. The interesting aspect of this problem is the definition of f (z)zα−1. Let

zα−1 ≡ e(ln|z|+iarg(z))(α−1) = e(α−1) log(z)

where arg(z) is the angle of z in (0,2π) . Thus you use a branch of the logarithm which isdefined on C\ (0,∞) . Then it is routine to verify from the assumed estimates that

limR→∞

∫γR

f (z)zα−1dz = 0

andlim

ε→0+

∫γε

f (z)zα−1dz = 0.

Also, it is routine to verify

limε→0+

∫γεR+

f (z)zα−1dz =∫ R

0f (x)xα−1dx

and

limε→0+

∫γεR−

f (z)zα−1dz =−ei2π(α−1)∫ R

0f (x)xα−1dx.