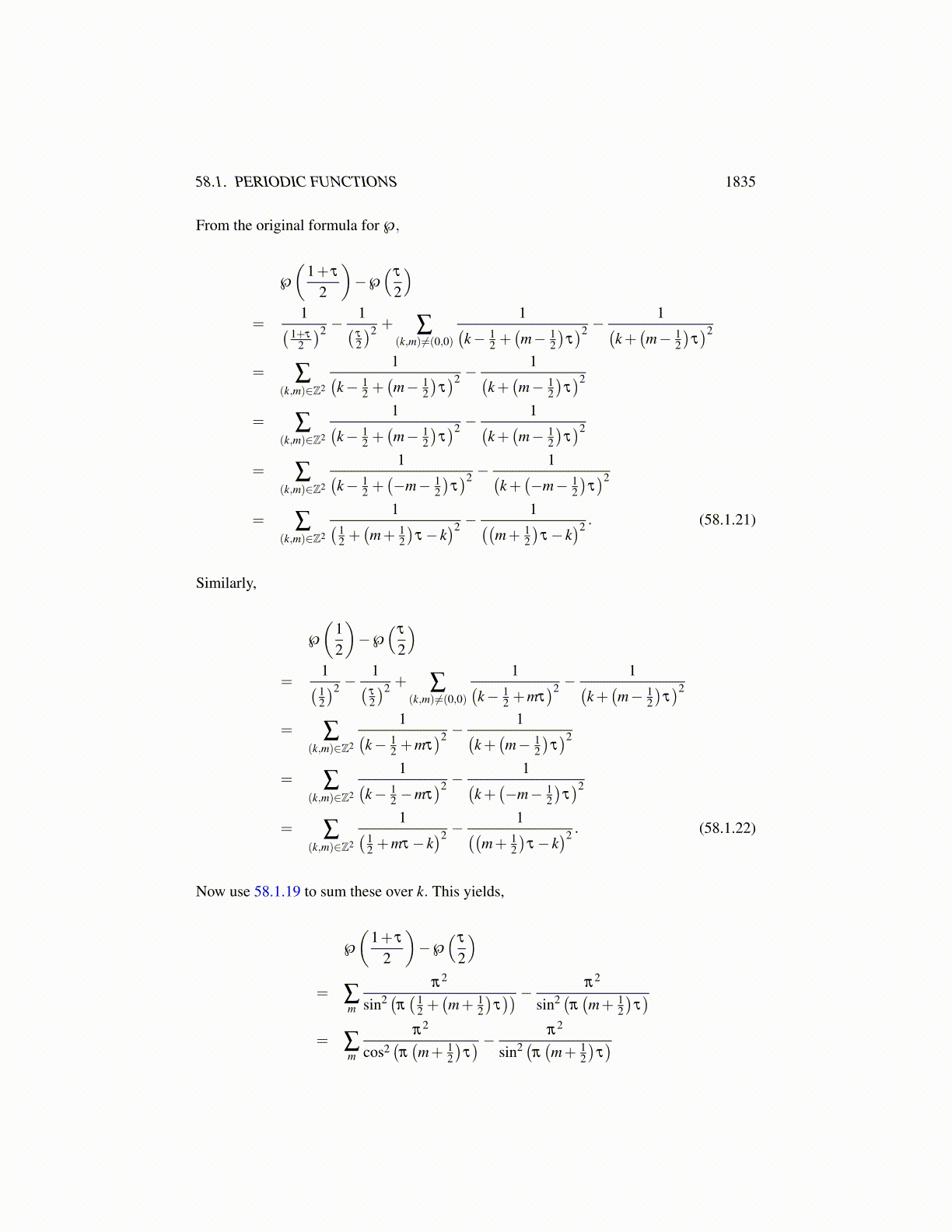
58.1. PERIODIC FUNCTIONS 1835
Hence τ ′ = w′2/w′1 = (w1 +w2)/w1 = 1+ τ . Then from the definition of λ ,
λ(τ′) = λ (1+ τ)
=℘
(w′1+w′2
2
)−℘
(w′22
)℘
(w′12
)−℘
(w′22
)=
℘(w1+w2+w1
2
)−℘
(w1+w22
)℘(w1
2
)−℘
(w1+w22
)=
℘(w2
2 +w1)−℘
(w1+w22
)℘(w1
2
)−℘
(w1+w22
)=
℘(w2
2
)−℘
(w1+w22
)℘(w1
2
)−℘
(w1+w22
)= −
℘(w1+w2
2
)−℘
(w22
)℘(w1
2
)−℘
(w1+w22
)= −
℘(w1+w2
2
)−℘
(w22
)℘(w1
2
)−℘
(w22
)+℘
(w22
)−℘
(w1+w22
)
= −
(℘
(w1+w2
2
)−℘(w2
2 )℘(w1
2 )−℘(w22 )
)
1+
(℘(w2
2 )−℘
(w1+w2
2
)℘(w1
2 )−℘(w22 )
)
=
(℘
(w1+w2
2
)−℘(w2
2 )℘(w1
2 )−℘(w22 )
)(
℘
(w1+w2
2
)−℘(w2
2 )℘(w1
2 )−℘(w22 )
)−1
=λ (τ)
λ (τ)−1. (58.1.16)
Summarizing the important feature of the above,
λ (1+ τ) =λ (τ)
λ (τ)−1. (58.1.17)
Next consider the other unimodular matrix in 58.1.15. In this case w′1 = w2 and w′2 = w1.
58.1. PERIODIC FUNCTIONS 1835Hence t! = w5/w) = (wi +w2) /w; = 1+. Then from the definition of 1,A(t’) = AC+7)o( 84) ~0(9)o()-0()e (Me) — ("3")(1) — (M4)e(F+wi)-e(7)(3) -0(45")3) p(s")= . 58.1.16A(t) -1 ( )Summarizing the important feature of the aboveA(t)A(1 = . 58.1.17Next consider the other unimodular matrix in 58.1.15. In this case wi = Ww» and ws =wy.