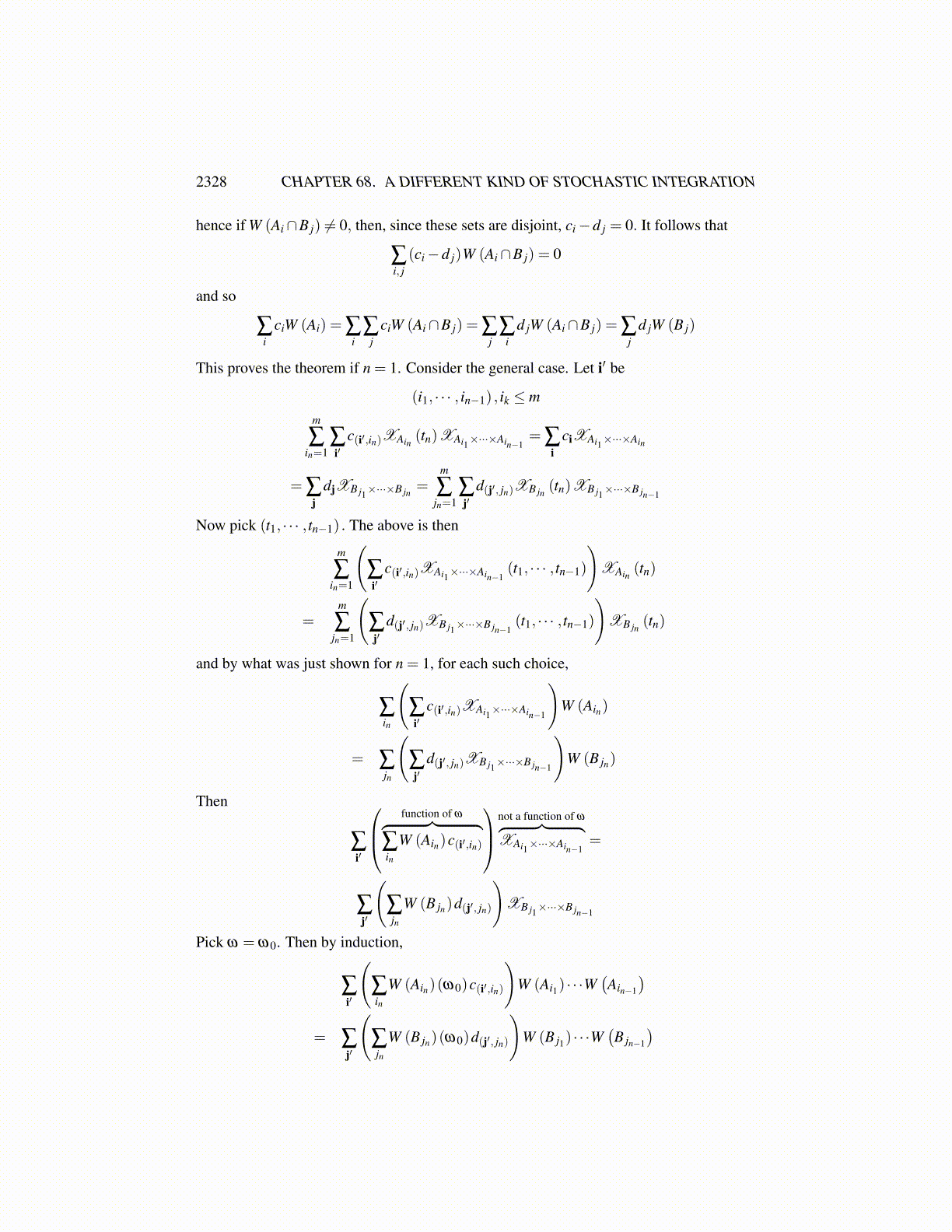
2328 CHAPTER 68. A DIFFERENT KIND OF STOCHASTIC INTEGRATION
Lemma 68.3.4 The following holds for f ∈ Em∥∥ f̃∥∥
L2(T m)≤ ∥ f∥L2(T m)
alsoIm ( f ) = Im
(f̃)
Proof: This follows because, thanks to the properties of Lebesgue measure,∫T m| f (t1, · · · , tm)|2 dt1 · · ·dtm =
∫T m| f (tσ1 , · · · , tσm)|
2 dt1 · · ·dtm
≡∫
T m| fσ |2 dt1 · · ·dtm
therefore, ∥∥ f̃∥∥
L2(T m)≤ 1
m! ∑σ∈Sm
∥ fσ∥L2(T m) =1
m! ∑σ∈Sm
∥ f∥L2(T m) = ∥ f∥L2(T m)
The next claim follows because on the right, the terms making up the sum just happen in adifferent order for each σ .
More generally, here is a lemma about off diagonal things. It uses sets Ai rather thanintervals [a,b).
Lemma 68.3.5 Let {A1, · · · ,Am} be pairwise disjoint sets in B (T ) each having finite mea-sure. Then the products Ai1 ×·· ·×Ain are pairwise disjoint. Also to say that the function
(t1, · · · , tn)→∑i
ciXAi1×···×Ain(t1, · · · , tn)
equals 0 whenever some t j = ti, i ̸= j is to say that ci = 0 whenever there is a repeated indexin i.
Proof: Suppose the condition that the Ak are pairwise disjoint holds and consider twoof these products, Ai1 × ·· · ×Ain and A j1 × ·· · ×A jn . If the two ordered lists (i1, · · · , in)and ( j1, · · · , jn) are different, then since the Ak are disjoint the two products have emptyintersection because they differ in some position.
Now suppose that ci = 0 whenever there is a repeated index. Then the sum is taken overall permutations of n things taken from {1, · · · ,m} and so if some tr = ts for r ̸= s, all termsof the sum equal zero because XAi1×···×Ain
̸= 0 only if t ∈ Ai1 ×·· ·×Ain and since tr = tsand the sets {Ak} are disjoint, there must be the same set in positions r and s so ci = 0.Hence the function equals 0.
Conversely, suppose the sum ∑i ciXAi1×···×Ainequals zero whenever some tr = ts for
s ̸= r. Does it follow that ci = 0 whenever some tr = ts? The value of this function att ∈ Ai1 ×·· ·×Ain is ci because for any other ordered list of indices, the resulting producthas empty intersecton with Ai1 ×·· ·×Ain . Thus, since tr = ts, it is given that this functionequals 0 which equals ci.