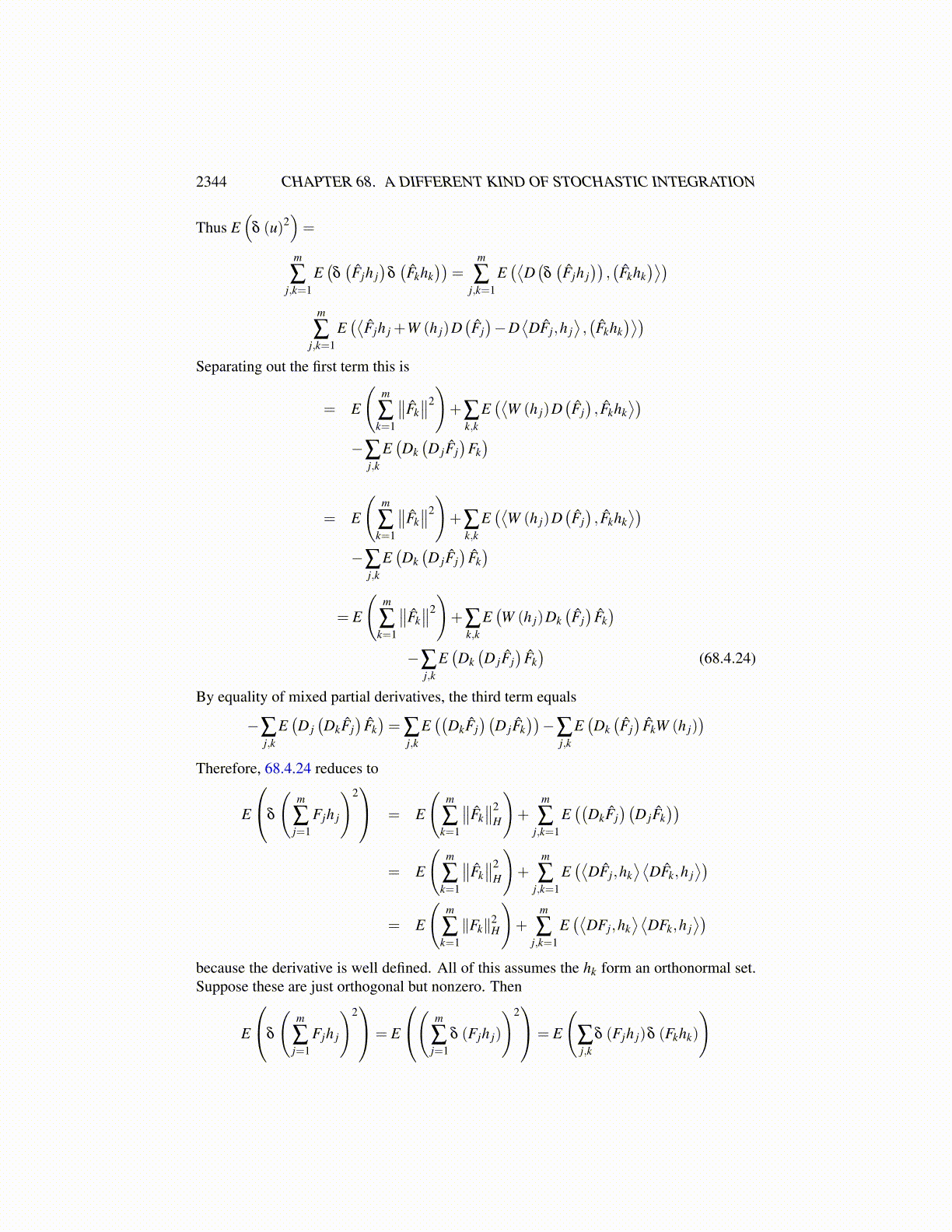
2344 CHAPTER 68. A DIFFERENT KIND OF STOCHASTIC INTEGRATION
Since δ is an adjoint map, it is clearly linear. Hence, if h is arbitrary, h ̸= 0 of course,
δ (Fh) = ∥h∥δ
(F(
W (h)∥h∥
))= ∥h∥F
W (h)∥h∥
−∥h∥n
∑i=1
Di (F)
(hi,
h∥h∥
)= FW (h)−
n
∑i=1
Di (F)(hi,h)H = FW (h)−⟨DF,h⟩ (68.4.22)
Note how this looks just like integration by parts. More generally,
δ
(m
∑j=1
Fjh j
)=
m
∑j=1
δ (Fjh j) =m
∑j=1
FjW (h j)−⟨DFj,h j
⟩Are functions like ∑
mj=1 Fjh j where Fj is a polynomial in variables of the form W (h)
dense in Lp (Ω,H)? It was shown earlier in Lemma 68.4.3 that polynomial functions F inthe W (h) are dense in Lp (Ω) for any p. Let s(ω) = ∑
nk=1 hkXEk be a simple function.
Then XEk is clearly in Lp (Ω) and so there exists Fk a polynomial in the W (h) which isas close as desired to XEk in Lp. Hence ∑
nk=1 hkFk is close to s in Lp (Ω,H) and so since
these simple functions are dense, it follows that these kinds of functions are indeed dense inLp (Ω,H), this for any p > 1. The above discussion is summarized in the following lemma.
Lemma 68.4.5 Functions of the form ∑nk=1 Fkhk where Fk is a polynomial in the W (h)
(Fj ∈P) are dense in Lp (Ω,H) for any p > 1. Also each function of this form is in Dδ
and
δ
(m
∑j=1
Fjh j
)=
m
∑j=1
δ (Fjh j) =m
∑j=1
FjW (h j)−⟨DFj,h j
⟩What does D do to δ (Fh)? It is shown above that δ (Fh) = FW (h)− ⟨DF,h⟩ . Say
F = F (W (h1) , · · · ,W (hn)) . Then when you do D to δ (Fh), you would get
Fh+n
∑k=1
Dk (F)W (h)hk−n
∑k=1
n
∑j=1
D j (Dk (F))h j (hk,h)
In other words,Fh+W (h)D(F)−D⟨DF,h⟩
Recall that DG is well defined. This means that we can replace {h1, · · · ,hn,h} with anorthonormal basis
{e1, · · · ,ep,h
}as in
G(W (h1) , · · · ,W (hn) ,W (h)) = Ĝ(W (e1) , · · · ,W (ep) ,W (h))
where we assume ∥h∥= 1 for simplicity. Thus the above equals
D(δ (F)) = D(δ(F̂))
= F̂h+W (h)D(F̂)−D
⟨DF̂ ,h
⟩Now consider E
(δ (Fh)2
)= E ⟨D(δ (Fh)) ,Fh⟩ . Thus the following must be considered.
E⟨F̂h+W (h)D
(F̂)−D
⟨DF̂ ,h
⟩, F̂h
⟩(68.4.23)