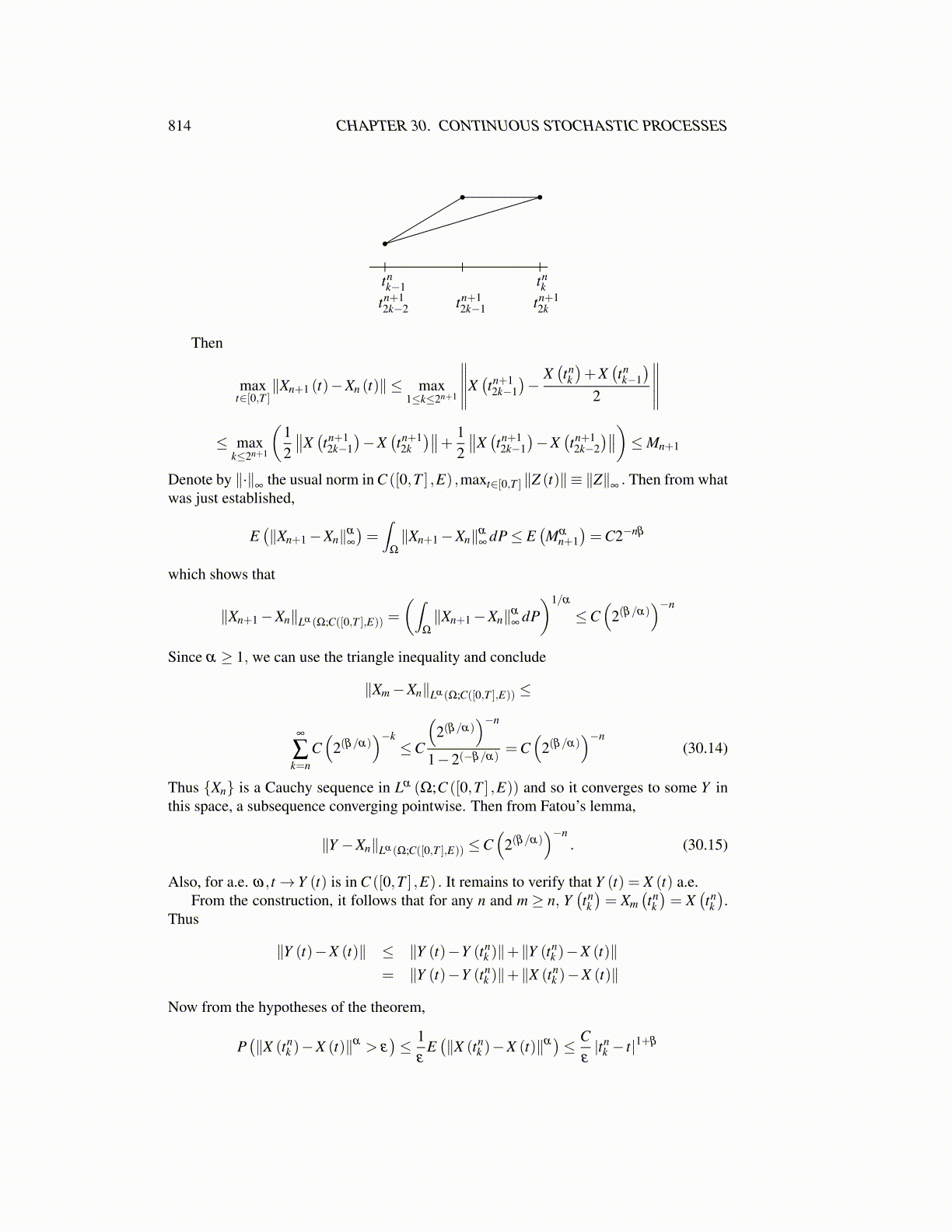
814 CHAPTER 30. CONTINUOUS STOCHASTIC PROCESSES
tnk−1 tn
ktn+12k−2 tn+1
2ktn+12k−1
Then
maxt∈[0,T ]
∥Xn+1 (t)−Xn (t)∥ ≤ max1≤k≤2n+1
∥∥∥∥∥X(tn+12k−1
)−
X(tnk
)+X
(tnk−1
)2
∥∥∥∥∥≤ max
k≤2n+1
(12
∥∥X(tn+12k−1
)−X
(tn+12k
)∥∥+ 12
∥∥X(tn+12k−1
)−X
(tn+12k−2
)∥∥)≤Mn+1
Denote by ∥·∥∞
the usual norm in C ([0,T ] ,E) ,maxt∈[0,T ] ∥Z (t)∥ ≡ ∥Z∥∞. Then from what
was just established,
E(∥Xn+1−Xn∥α
∞
)=∫
Ω
∥Xn+1−Xn∥α
∞dP≤ E
(Mα
n+1)=C2−nβ
which shows that
∥Xn+1−Xn∥Lα (Ω;C([0,T ],E)) =
(∫Ω
∥Xn+1−Xn∥α
∞dP)1/α
≤C(
2(β/α))−n
Since α ≥ 1, we can use the triangle inequality and conclude
∥Xm−Xn∥Lα (Ω;C([0,T ],E)) ≤
∞
∑k=n
C(
2(β/α))−k≤C
(2(β/α)
)−n
1−2(−β/α)=C
(2(β/α)
)−n(30.14)
Thus {Xn} is a Cauchy sequence in Lα (Ω;C ([0,T ] ,E)) and so it converges to some Y inthis space, a subsequence converging pointwise. Then from Fatou’s lemma,
∥Y −Xn∥Lα (Ω;C([0,T ],E)) ≤C(
2(β/α))−n
. (30.15)
Also, for a.e. ω, t→ Y (t) is in C ([0,T ] ,E) . It remains to verify that Y (t) = X (t) a.e.From the construction, it follows that for any n and m ≥ n, Y
(tnk
)= Xm
(tnk
)= X
(tnk
).
Thus
∥Y (t)−X (t)∥ ≤ ∥Y (t)−Y (tnk )∥+∥Y (tn
k )−X (t)∥= ∥Y (t)−Y (tn
k )∥+∥X (tnk )−X (t)∥
Now from the hypotheses of the theorem,
P(∥X (tn
k )−X (t)∥α > ε)≤ 1
εE(∥X (tn
k )−X (t)∥α)≤ C
ε|tn
k − t|1+β