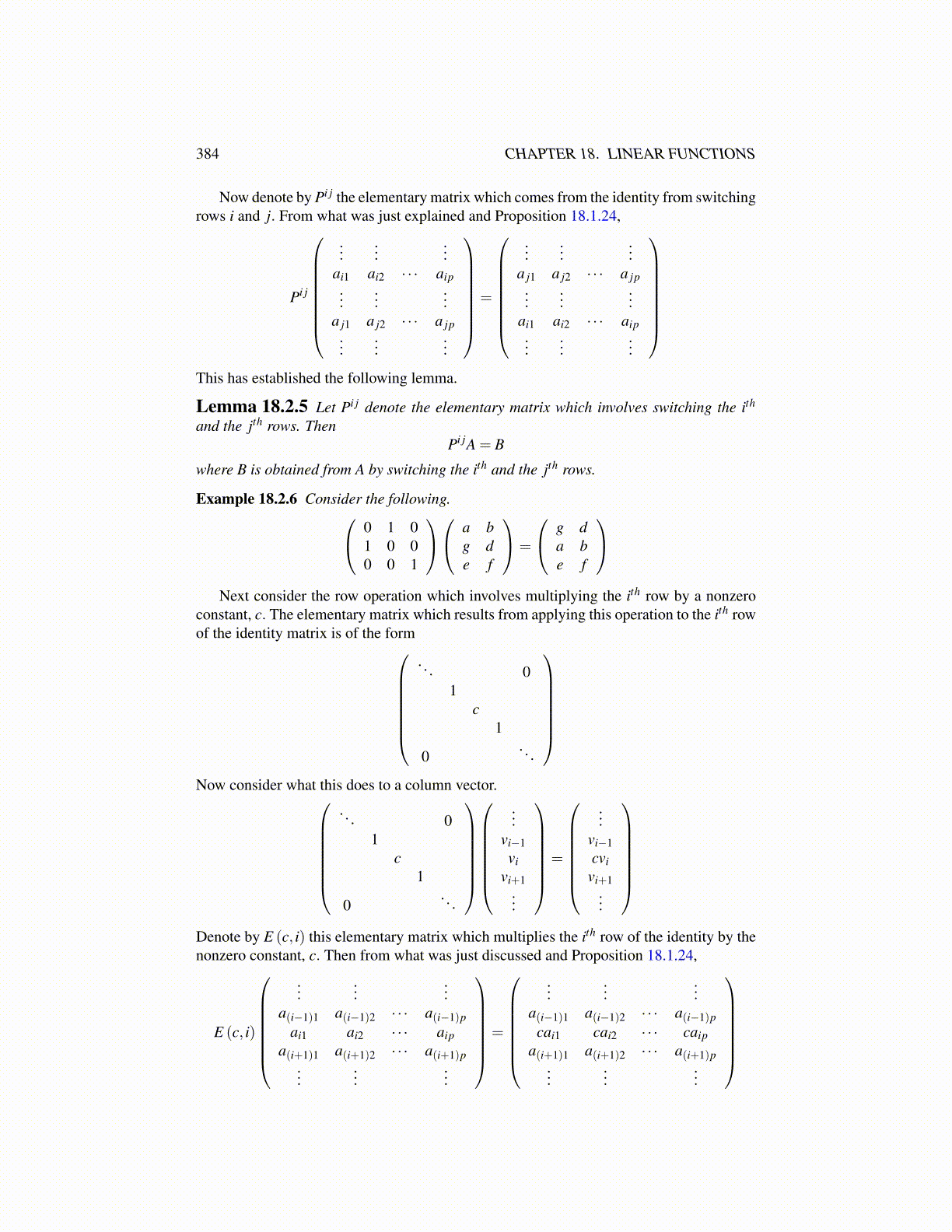
384 CHAPTER 18. LINEAR FUNCTIONS
Lemma 18.2.9 Let E (c× i+ j) denote the elementary matrix obtained from I by re-placing the jth row with c times the ith row added to it. Then
E (c× i+ j)A = B
where B is obtained from A by replacing the jth row of A with itself added to c times the ith
row of A.
Example 18.2.10 Consider the third row operation. 1 0 00 1 02 0 1
a bc de f
=
a bc d
2a+ e 2b+ f
The next theorem is the main result.
Theorem 18.2.11 To perform any of the three row operations on a matrix A, itsuffices to do the row operation on the identity matrix obtaining an elementary matrix Eand then take the product, EA. Furthermore, if E is an elementary matrix, then there isanother elementary matrix Ê such that EÊ = ÊE = I.
Proof: The first part of this theorem has been proved in Lemmas 18.2.5 - 18.2.9. Itonly remains to verify the claim about the matrix Ê. Consider first the elementary matricescorresponding to row operation of type three.
E (−c× i+ j)E (c× i+ j) = I.
This follows because the first matrix takes c times row i in the identity and adds it to row j.When multiplied on the left by E (−c× i+ j) it follows from the first part of this theoremthat you take the ith row of E (c× i+ j) which coincides with the ith row of I since that rowwas not changed, multiply it by −c and add to the jth row of E (c× i+ j) which was thejth row of I added to c times the ith row of I. Thus E (−c× i+ j) multiplied on the left,undoes the row operation which resulted in E (c× i+ j). The same argument applied tothe product E (c× i+ j)E (−c× i+ j) replacing c with −c in the argument yields that thisproduct is also equal to I. Therefore, there is an elementary matrix of the same sort whichwhen multiplied by E on either side gives the identity.
Similar reasoning shows that for E (c, i) the elementary matrix which comes from mul-tiplying the ith row by the nonzero constant c, you can take Ê = E ((1/c) , i).
Finally, consider Pi j which involves switching the ith and the jth rows Pi jPi j = I be-cause by the first part of this theorem, multiplying on the left by Pi j switches the ith and jth
rows of Pi j which was obtained from switching the ith and jth rows of the identity. Firstyou switch them to get Pi j and then you multiply on the left by Pi j which switches theserows again and restores the identity matrix.
The way we solve the linear equation Ax= b is to multiply on both sides by a suc-cession of elementary matrices, in other words do row operations to both sides until thesolution is obvious.
Proposition 18.2.12 The solution set to Ax= b is unchanged if the same row opera-tion is done to A as to b. In other words, it has the same solution set as EAx= Eb.