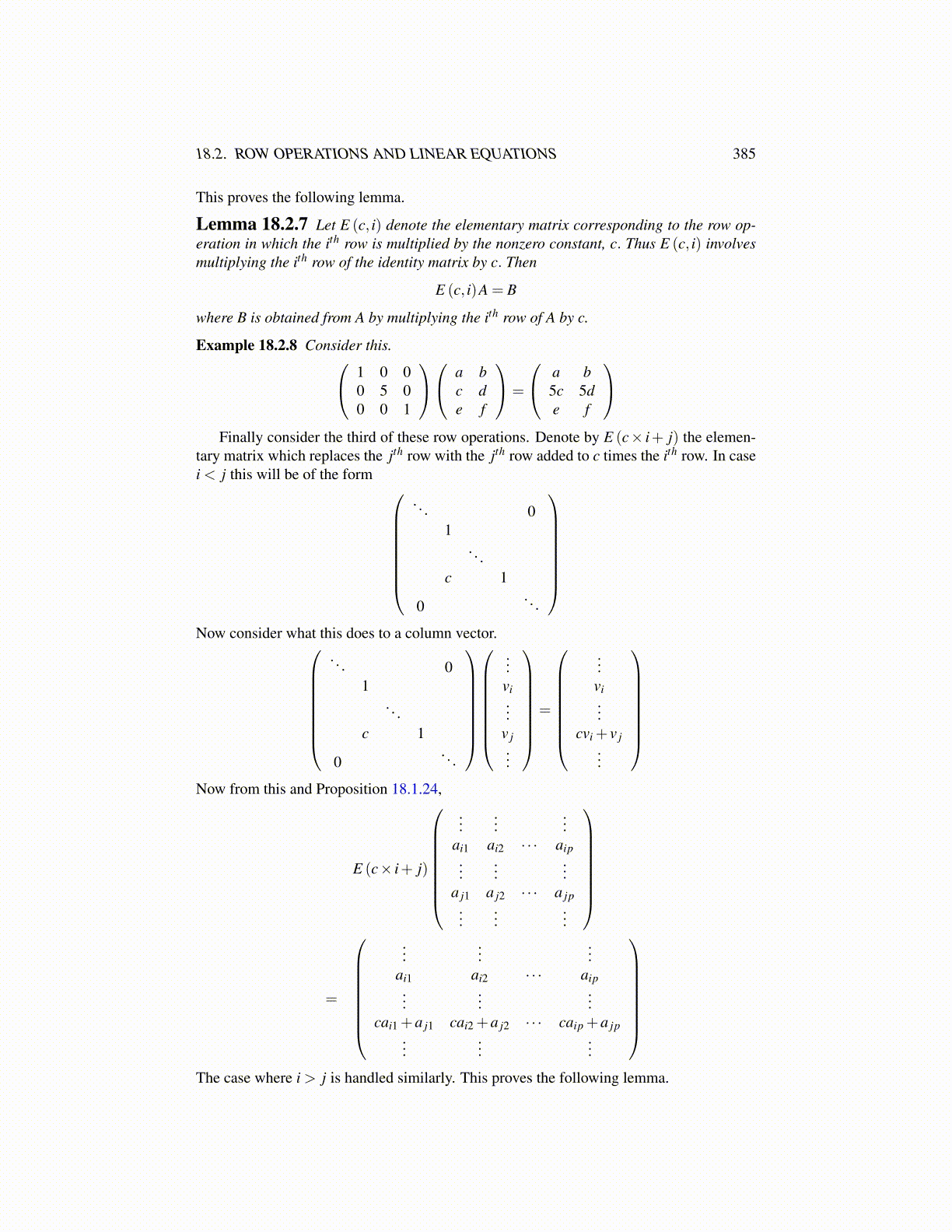
18.2. ROW OPERATIONS AND LINEAR EQUATIONS 385
Proof: If x is such that EAx = Eb then use the Ê of the above Theorem 18.2.11 mul-tiply both sides by Ê and use the associative law to obtain Ax = Ê (EA)x = ÊEb= b. IfAx= b, then EAx= Eb. Thus the two systems have the same solution set.
More generally, it is convenient to consider such a system in the form (A|b) where thematrix A is on the left and there is another column b to give the last column. Such a matrixis called an augmented matrix. Then solving the system Ax= b is equivalent to findingb as a linear combination of the columns of A. In other words, you want to find a linearrelationship between b and the other columns. You are doing the same row operations onA as on b and so you might as well consider the system in this shortened form.
Example 18.2.13 Solve (1 1 11 2 −1
) xyz
=
(1−5
)You consider (
1 1 1 11 2 −1 −5
)Now proceed to do row operations. Take −1 times the top row and add to the bottom.(
1 1 1 10 1 −2 −6
)Now take −1 times the bottom and add to the top.(
1 0 3 70 1 −2 −6
)At this point it is obvious. Write as equations. You have x+3z = 7,y−2z =−6. You cantherefore, pick z to be anything. I shall let it equal t. Then a solution is of the form
x = 7−3t, y =−6+2t, z = t, t ∈ R
The solution is given parametrically in this form. Remember parametric lines. In this case,there is an infinite selection of solutions.
Example 18.2.14 Find the solution to 2 2 31 1 02 2 2
xyz
=
334
Do it the same. 2 2 3 3
1 1 0 32 2 2 4
Now do row operations to this matrix to get 1 1 0 3
0 0 1 −10 0 0 0
Thus x = 3− t,y = t,z =−1 and t ∈ R.