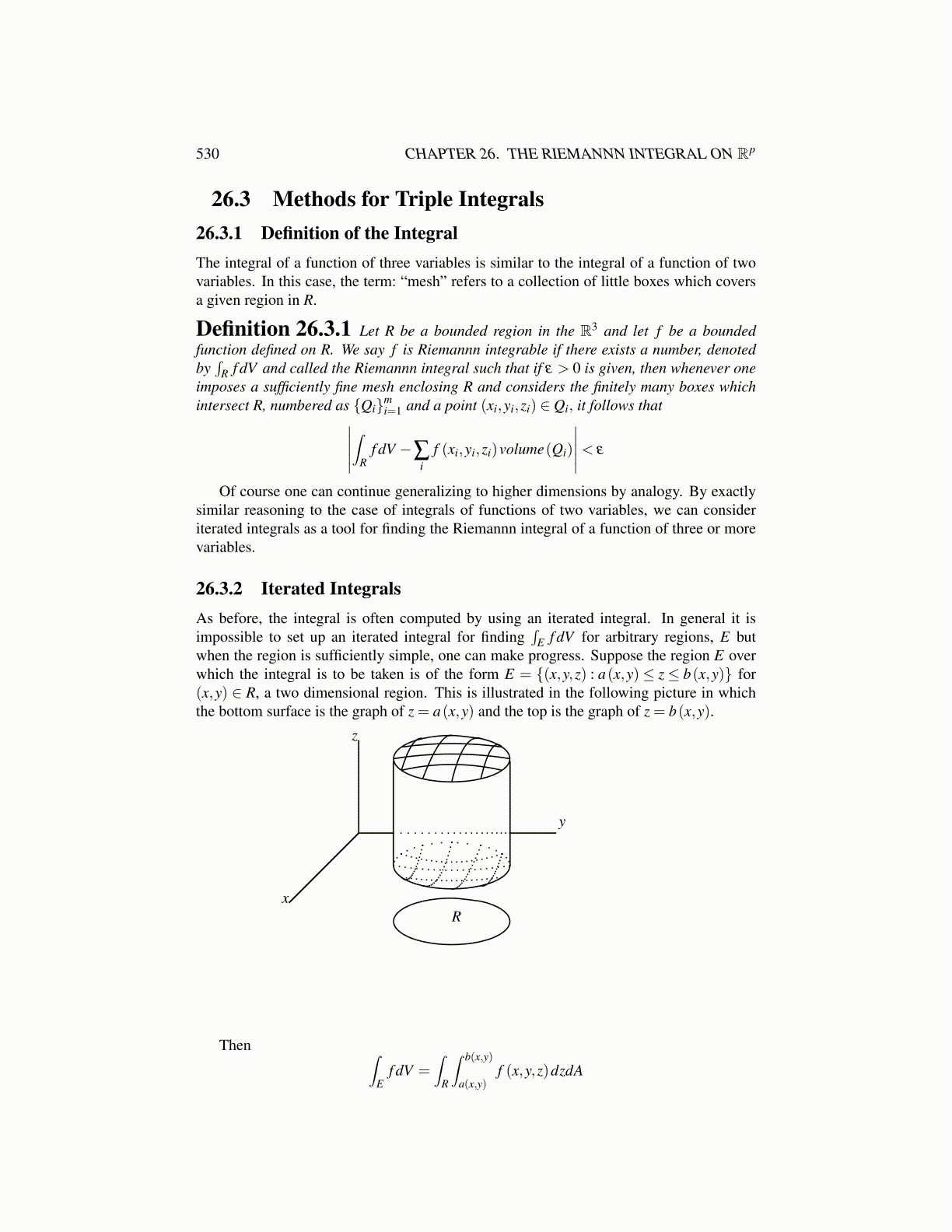
530 CHAPTER 26. THE RIEMANNN INTEGRAL ON Rp
In the yz plane, the first of the following pictures corresponds to x = 0.
3y+3z = 2
23
23
y(0,0,0)
z
x = 16− y2
Therefore, the outside integrals taken with respect to z and y are of the form∫ 23
0
∫ 23−y
0dzdy
and now for any choice of (y,z) in the above triangular region, x goes from 0 to 16− y2.Therefore, the iterated integral is∫ 2
3
0
∫ 23−y
0
∫ 16−y2
0dxdzdy =
860243
Example 26.3.7 Find the volume of the region determined by the intersection of the twocylinders, x2 + y2 ≤ 1 and x2 + z2 ≤ 1.
The first listed cylinder intersects the xy plane in the disk, x2 + y2 ≤ 1. What is thevolume of the three dimensional region which is between this disk and the two surfaces,z =
√1− x2 and z =−
√1− x2? An iterated integral for the volume is
∫ 1
−1
∫ √1−x2
−√
1−x2
∫ √1−x2
−√
1−x2dzdydx =
163.
Note that I drew no picture of the three dimensional region. If you are interested, here it is.
One of the cylinders is parallel to the z axis, x2 + y2 ≤ 1 and the other is parallel to they axis, x2 + z2 ≤ 1. I did not need to be able to draw such a nice picture in order to workthis problem. This is the key to doing these. Draw pictures in two dimensions and reasonfrom the two dimensional pictures rather than attempt to wax artistic and consider all threedimensions at once. These problems are hard enough without making them even harder byattempting to be an artist.