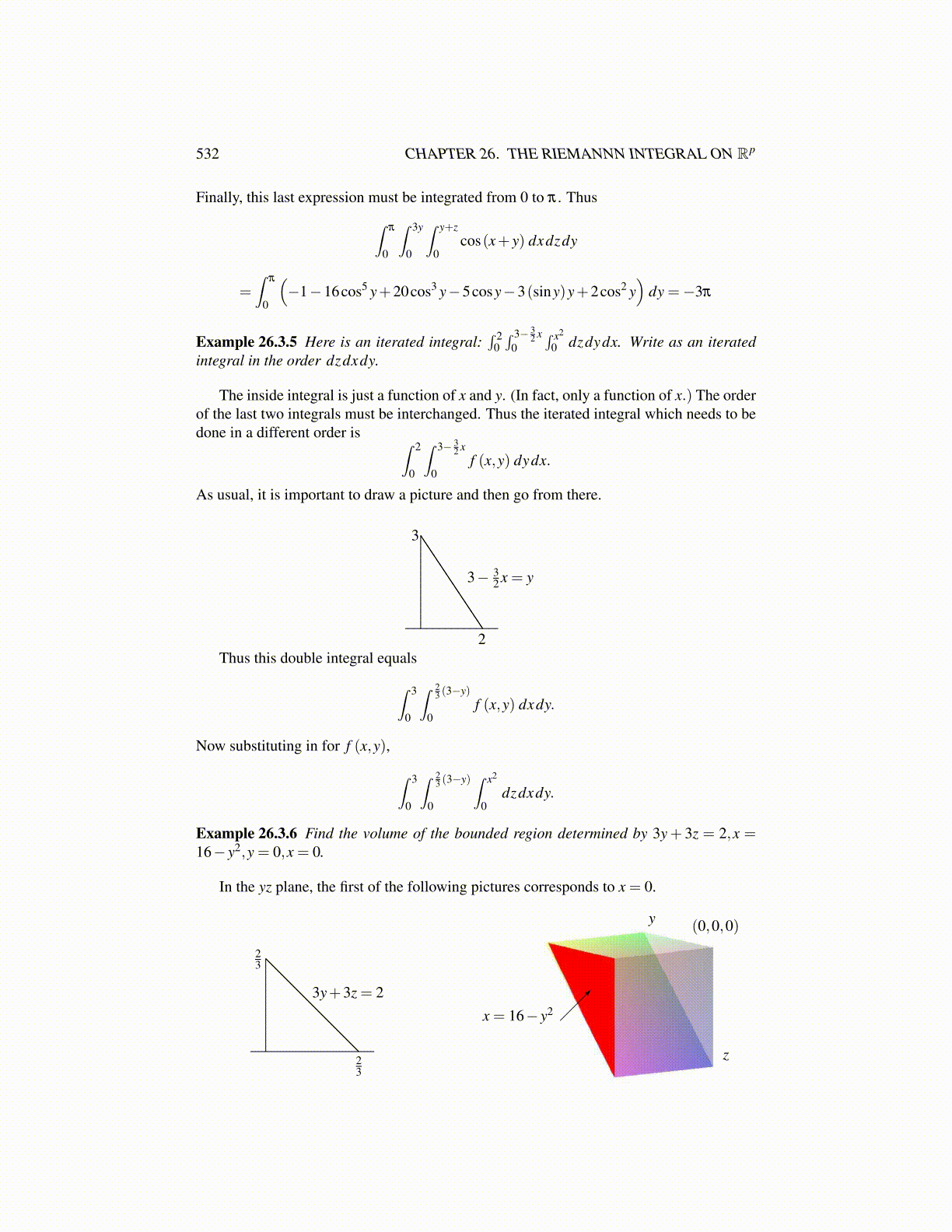
532 CHAPTER 26. THE RIEMANNN INTEGRAL ON Rp

13. Find the volume of the region bounded by x2 + y2 = 25,z = x,z = 0, and x ≥ 0.

Your answer should be 2503 .

14. Find the volume of the region bounded by x2 + y2 = 9,z = 3x,z = 0, and x ≥ 0.

26.4.1 Mass and DensityAs an example of the use of triple integrals, consider a solid occupying a set of pointsU ⊆ R3 having density ρ . Thus ρ is a function of position and the total mass of the solidequals

∫U ρ dV . This is just like the two dimensional case. The mass of an infinitesimal

chunk of the solid located at x would be ρ (x) dV and so the total mass is just the sum ofall these,

∫U ρ (x) dV .

Example 26.4.1 Find the volume of R where R is the bounded region formed by the plane15 x+ y+ 1

5 z = 1 and the planes x = 0,y = 0,z = 0.

When z = 0, the plane becomes 15 x+y = 1. Thus the intersection of this plane with the

xy plane is this line shown in the following picture.

1

5Therefore, the bounded region is between the triangle formed in the above picture by

the x axis, the y axis and the above line and the surface given by 15 x+ y+ 1

5 z = 1 or z =5(1−( 1

5 x+ y))

= 5− x−5y. Therefore, an iterated integral which yields the volume is

∫ 5

0

∫ 1− 15 x

0

∫ 5−x−5y

0dzdydx =

256.

Example 26.4.2 Find the mass of the bounded region R formed by the plane 13 x+ 1

3 y+ 15 z=

1 and the planes x = 0,y = 0,z = 0 if the density is ρ (x,y,z) = z.

This is done just like the previous example except in this case, there is a function tointegrate. Thus the answer is

∫ 3

0

∫ 3−x

0

∫ 5− 53 x− 5

3 y

0z dzdydx =

758.

Example 26.4.3 Find the total mass of the bounded solid determined by z = 9− x2 − y2

and x,y,z ≥ 0 if the mass is given by ρ (x,y,z) = z

When z = 0 the surface z = 9− x2 − y2 intersects the xy plane in a circle of radius 3centered at (0,0). Since x,y ≥ 0, it is only a quarter of a circle of interest, the part whereboth these variables are nonnegative. For each (x,y) inside this quarter circle, z goes from0 to 9− x2 − y2. Therefore, the iterated integral is of the form,

∫ 3

0

∫ √(9−x2)

0

∫ 9−x2−y2

0z dzdydx =

2438

π