68 CHAPTER 2. FUNCTIONS
c
c
a
b
a
b
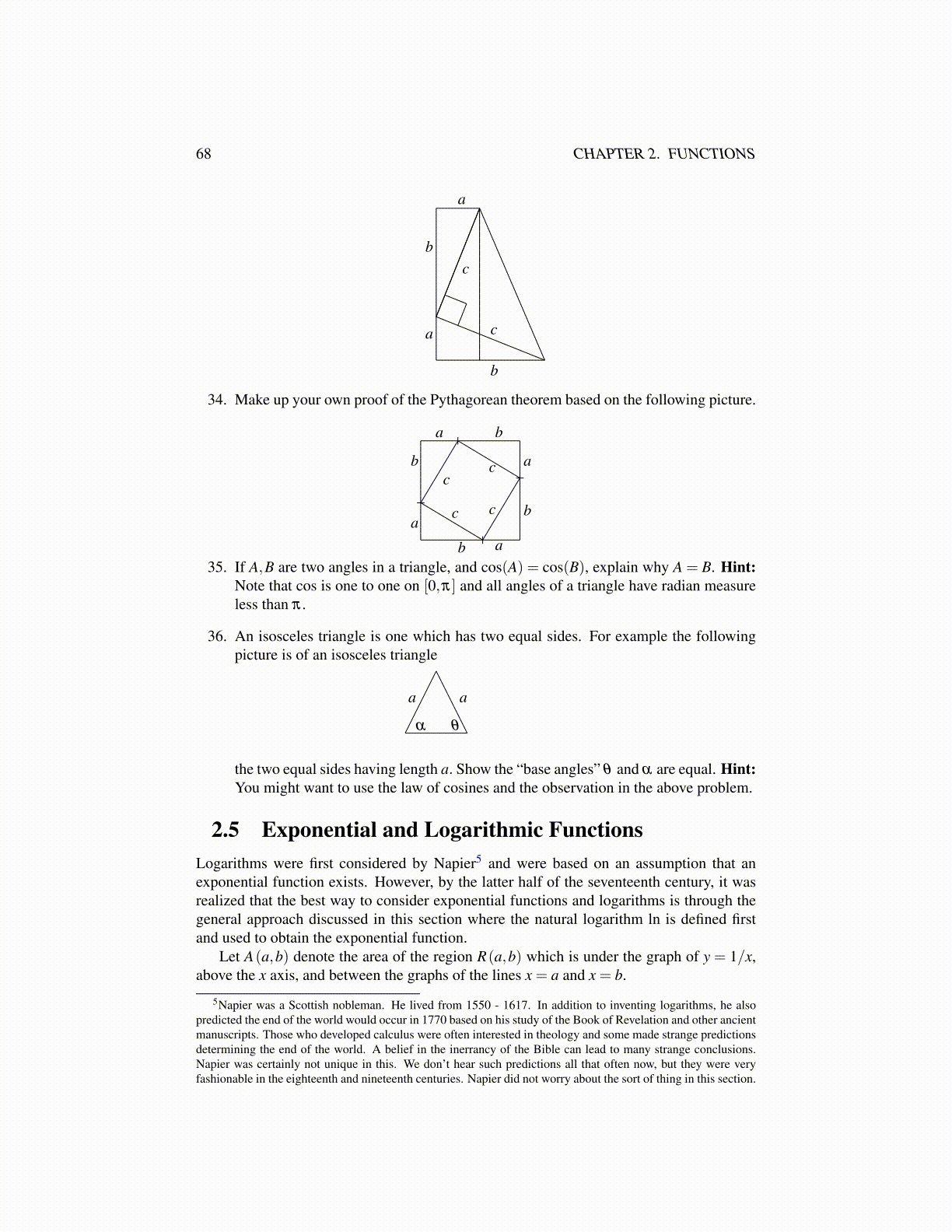
34. Make up your own proof of the Pythagorean theorem based on the following picture.
c
c
c
c b
b
b a
b a
a
a
35. If A,B are two angles in a triangle, and cos(A) = cos(B), explain why A = B. Hint:Note that cos is one to one on [0,π] and all angles of a triangle have radian measureless than π .
36. An isosceles triangle is one which has two equal sides. For example the followingpicture is of an isosceles triangle
θα
aa
the two equal sides having length a. Show the “base angles” θ and α are equal. Hint:You might want to use the law of cosines and the observation in the above problem.
2.5 Exponential and Logarithmic FunctionsLogarithms were first considered by Napier5 and were based on an assumption that anexponential function exists. However, by the latter half of the seventeenth century, it wasrealized that the best way to consider exponential functions and logarithms is through thegeneral approach discussed in this section where the natural logarithm ln is defined firstand used to obtain the exponential function.
Let A(a,b) denote the area of the region R(a,b) which is under the graph of y = 1/x,above the x axis, and between the graphs of the lines x = a and x = b.
5Napier was a Scottish nobleman. He lived from 1550 - 1617. In addition to inventing logarithms, he alsopredicted the end of the world would occur in 1770 based on his study of the Book of Revelation and other ancientmanuscripts. Those who developed calculus were often interested in theology and some made strange predictionsdetermining the end of the world. A belief in the inerrancy of the Bible can lead to many strange conclusions.Napier was certainly not unique in this. We don’t hear such predictions all that often now, but they were veryfashionable in the eighteenth and nineteenth centuries. Napier did not worry about the sort of thing in this section.