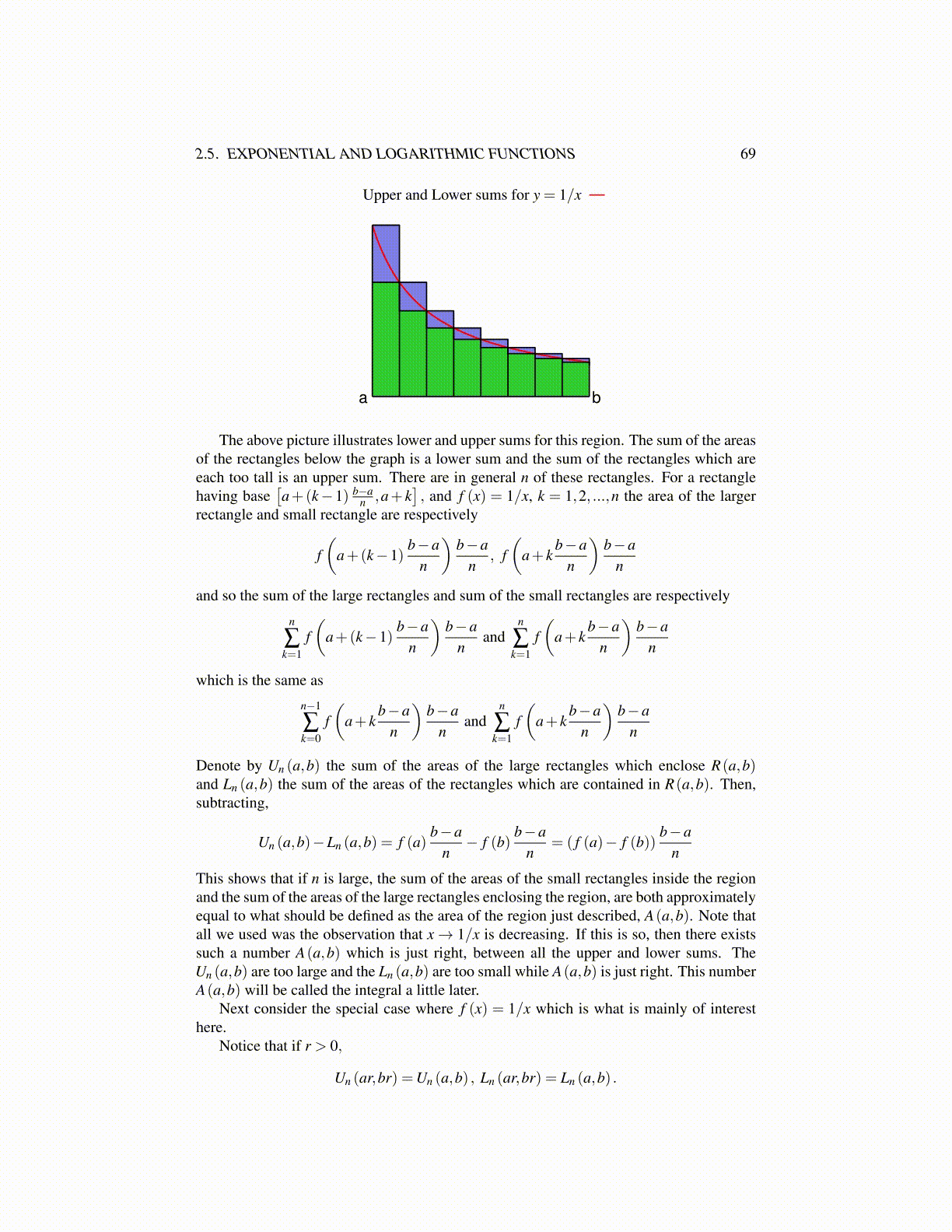
2.5. EXPONENTIAL AND LOGARITHMIC FUNCTIONS 69
Upper and Lower sums for y = 1/x
a b
The above picture illustrates lower and upper sums for this region. The sum of the areasof the rectangles below the graph is a lower sum and the sum of the rectangles which areeach too tall is an upper sum. There are in general n of these rectangles. For a rectanglehaving base
[a+(k−1) b−a
n ,a+ k], and f (x) = 1/x, k = 1,2, ...,n the area of the larger
rectangle and small rectangle are respectively
f(
a+(k−1)b−a
n
)b−a
n, f(
a+ kb−a
n
)b−a
n
and so the sum of the large rectangles and sum of the small rectangles are respectively
n
∑k=1
f(
a+(k−1)b−a
n
)b−a
nand
n
∑k=1
f(
a+ kb−a
n
)b−a
n
which is the same as
n−1
∑k=0
f(
a+ kb−a
n
)b−a
nand
n
∑k=1
f(
a+ kb−a
n
)b−a
n
Denote by Un (a,b) the sum of the areas of the large rectangles which enclose R(a,b)and Ln (a,b) the sum of the areas of the rectangles which are contained in R(a,b). Then,subtracting,
Un (a,b)−Ln (a,b) = f (a)b−a
n− f (b)
b−an
= ( f (a)− f (b))b−a
n
This shows that if n is large, the sum of the areas of the small rectangles inside the regionand the sum of the areas of the large rectangles enclosing the region, are both approximatelyequal to what should be defined as the area of the region just described, A(a,b). Note thatall we used was the observation that x → 1/x is decreasing. If this is so, then there existssuch a number A(a,b) which is just right, between all the upper and lower sums. TheUn (a,b) are too large and the Ln (a,b) are too small while A(a,b) is just right. This numberA(a,b) will be called the integral a little later.
Next consider the special case where f (x) = 1/x which is what is mainly of interesthere.
Notice that if r > 0,
Un (ar,br) =Un (a,b) , Ln (ar,br) = Ln (a,b) .