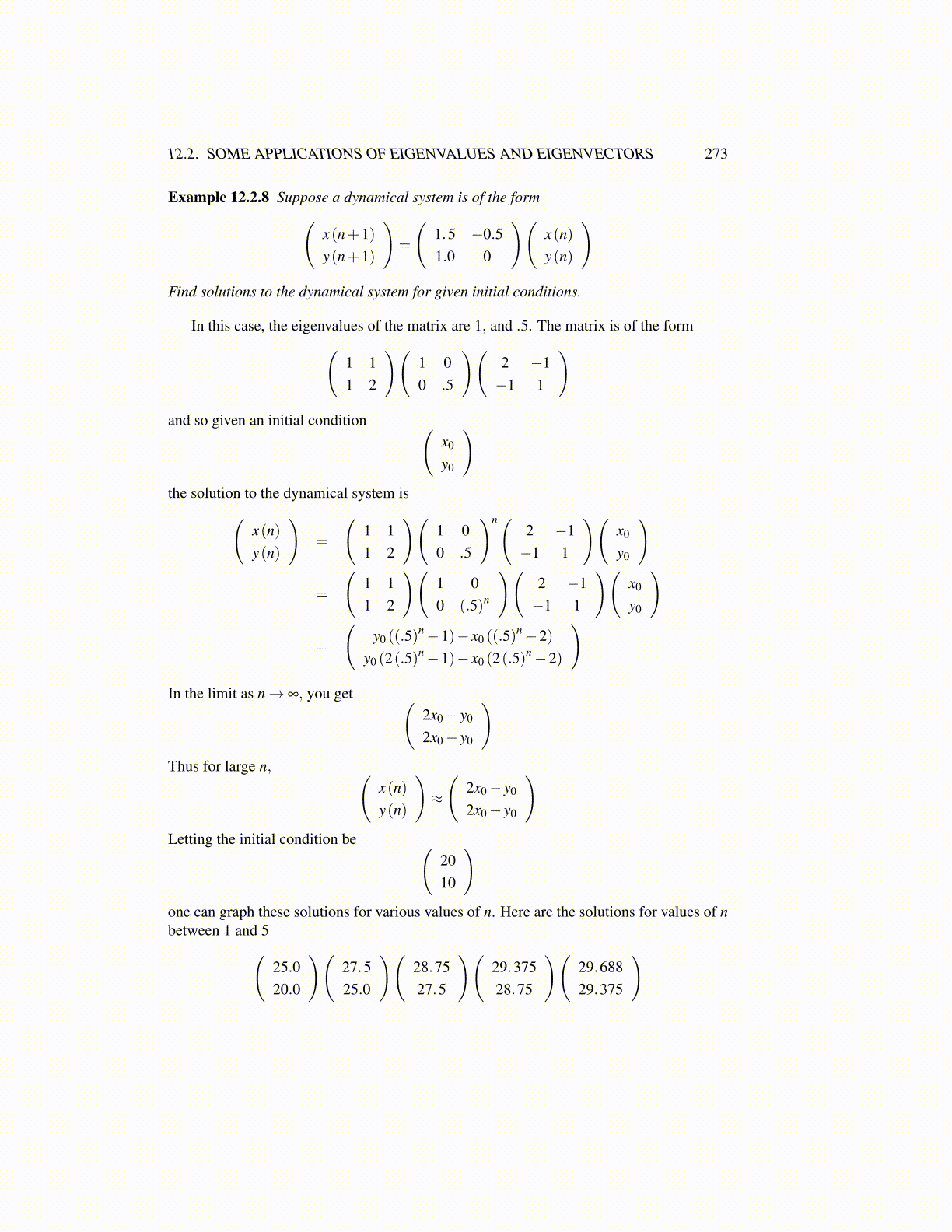
12.2. SOME APPLICATIONS OF EIGENVALUES AND EIGENVECTORS 273
Example 12.2.8 Suppose a dynamical system is of the form(x(n+1)y(n+1)
)=
(1.5 −0.51.0 0
)(x(n)y(n)
)
Find solutions to the dynamical system for given initial conditions.
In this case, the eigenvalues of the matrix are 1, and .5. The matrix is of the form(1 11 2
)(1 00 .5
)(2 −1−1 1
)
and so given an initial condition (x0
y0
)the solution to the dynamical system is(
x(n)y(n)
)=
(1 11 2
)(1 00 .5
)n(2 −1−1 1
)(x0
y0
)
=
(1 11 2
)(1 00 (.5)n
)(2 −1−1 1
)(x0
y0
)
=
(y0 ((.5)
n−1)− x0 ((.5)n−2)
y0 (2(.5)n−1)− x0 (2(.5)
n−2)
)
In the limit as n→ ∞, you get (2x0− y0
2x0− y0
)Thus for large n, (
x(n)y(n)
)≈
(2x0− y0
2x0− y0
)Letting the initial condition be (
2010
)one can graph these solutions for various values of n. Here are the solutions for values of nbetween 1 and 5(
25.020.0
)(27.525.0
)(28.7527.5
)(29.37528.75
)(29.68829.375
)