17.7. EXERCISES 417

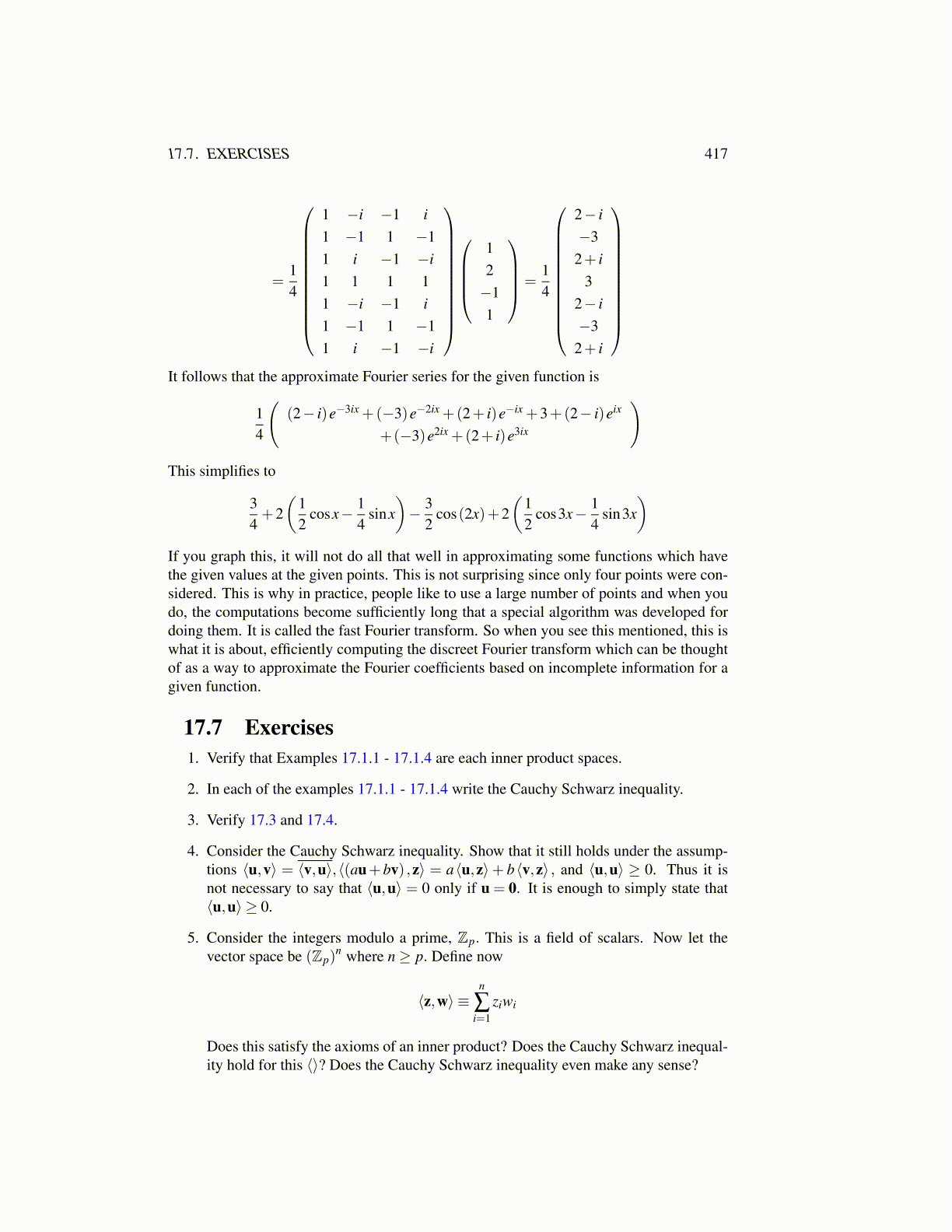
=14



1 −i −1 i1 −1 1 −11 i −1 −i1 1 1 11 −i −1 i1 −1 1 −11 i −1 −i



12−11

=14



2− i−3

2+ i3

2− i−3

2+ i

It follows that the approximate Fourier series for the given function is

14

((2− i)e−3ix +(−3)e−2ix +(2+ i)e−ix +3+(2− i)eix

+(−3)e2ix +(2+ i)e3ix

)

This simplifies to

34+2(

12

cosx− 14

sinx)− 3

2cos(2x)+2

(12

cos3x− 14

sin3x)

If you graph this, it will not do all that well in approximating some functions which havethe given values at the given points. This is not surprising since only four points were con-sidered. This is why in practice, people like to use a large number of points and when youdo, the computations become sufficiently long that a special algorithm was developed fordoing them. It is called the fast Fourier transform. So when you see this mentioned, this iswhat it is about, efficiently computing the discreet Fourier transform which can be thoughtof as a way to approximate the Fourier coefficients based on incomplete information for agiven function.

17.7 Exercises1. Verify that Examples 17.1.1 - 17.1.4 are each inner product spaces.

2. In each of the examples 17.1.1 - 17.1.4 write the Cauchy Schwarz inequality.

3. Verify 17.3 and 17.4.

4. Consider the Cauchy Schwarz inequality. Show that it still holds under the assump-tions ⟨u,v⟩ = ⟨v,u⟩,⟨(au+bv) ,z⟩ = a⟨u,z⟩+ b⟨v,z⟩ , and ⟨u,u⟩ ≥ 0. Thus it isnot necessary to say that ⟨u,u⟩ = 0 only if u = 0. It is enough to simply state that⟨u,u⟩ ≥ 0.

5. Consider the integers modulo a prime, Zp. This is a field of scalars. Now let thevector space be (Zp)

n where n≥ p. Define now

⟨z,w⟩ ≡n

∑i=1

ziwi

Does this satisfy the axioms of an inner product? Does the Cauchy Schwarz inequal-ity hold for this ⟨⟩? Does the Cauchy Schwarz inequality even make any sense?