356 CHAPTER 19. THE RIEMANNN INTEGRAL ON Rn

Definition 19.3.1 Let R be a bounded region in the R3 and let f be a bounded functiondefined on R. We say f is Riemannn integrable if there exists a number, denoted by

∫R f dV

and called the Riemannn integral such that if ε > 0 is given, then whenever one imposes asufficiently fine mesh enclosing R and considers the finitely many boxes which intersect R,numbered as {Qi}m

i=1 and a point (xi,yi,zi) ∈ Qi, it follows that∣∣∣∣∣∫

Rf dV −∑

if (xi,yi,zi)volume(Qi)

∣∣∣∣∣< ε

Of course one can continue generalizing to higher dimensions by analogy. By exactlysimilar reasoning to the case of integrals of functions of two variables, we can consideriterated integrals as a tool for finding the Riemannn integral of a function of three or morevariables.

19.3.2 Iterated IntegralsAs before, the integral is often computed by using an iterated integral. In general it isimpossible to set up an iterated integral for finding

∫E f dV for arbitrary regions, E but

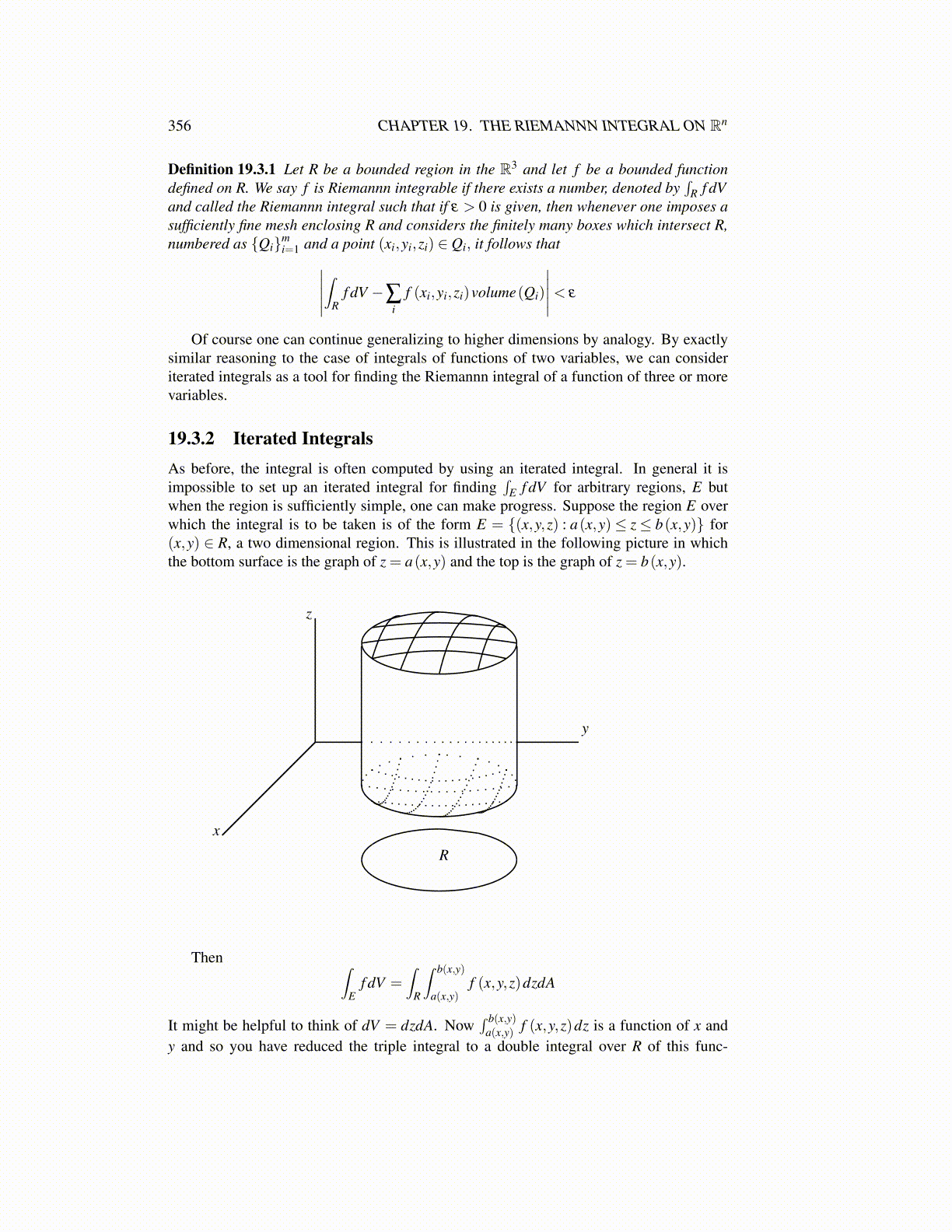
when the region is sufficiently simple, one can make progress. Suppose the region E overwhich the integral is to be taken is of the form E = {(x,y,z) : a(x,y)≤ z≤ b(x,y)} for(x,y) ∈ R, a two dimensional region. This is illustrated in the following picture in whichthe bottom surface is the graph of z = a(x,y) and the top is the graph of z = b(x,y).

x

z

y

R

Then ∫E

f dV =∫

R

∫ b(x,y)

a(x,y)f (x,y,z)dzdA

It might be helpful to think of dV = dzdA. Now∫ b(x,y)

a(x,y) f (x,y,z)dz is a function of x andy and so you have reduced the triple integral to a double integral over R of this func-