19.3. METHODS FOR TRIPLE INTEGRALS 357
tion of x and y. Similar reasoning would apply if the region in R3 were of the form{(x,y,z) : a(y,z)≤ x≤ b(y,z)} or {(x,y,z) : a(x,z)≤ y≤ b(x,z)}.
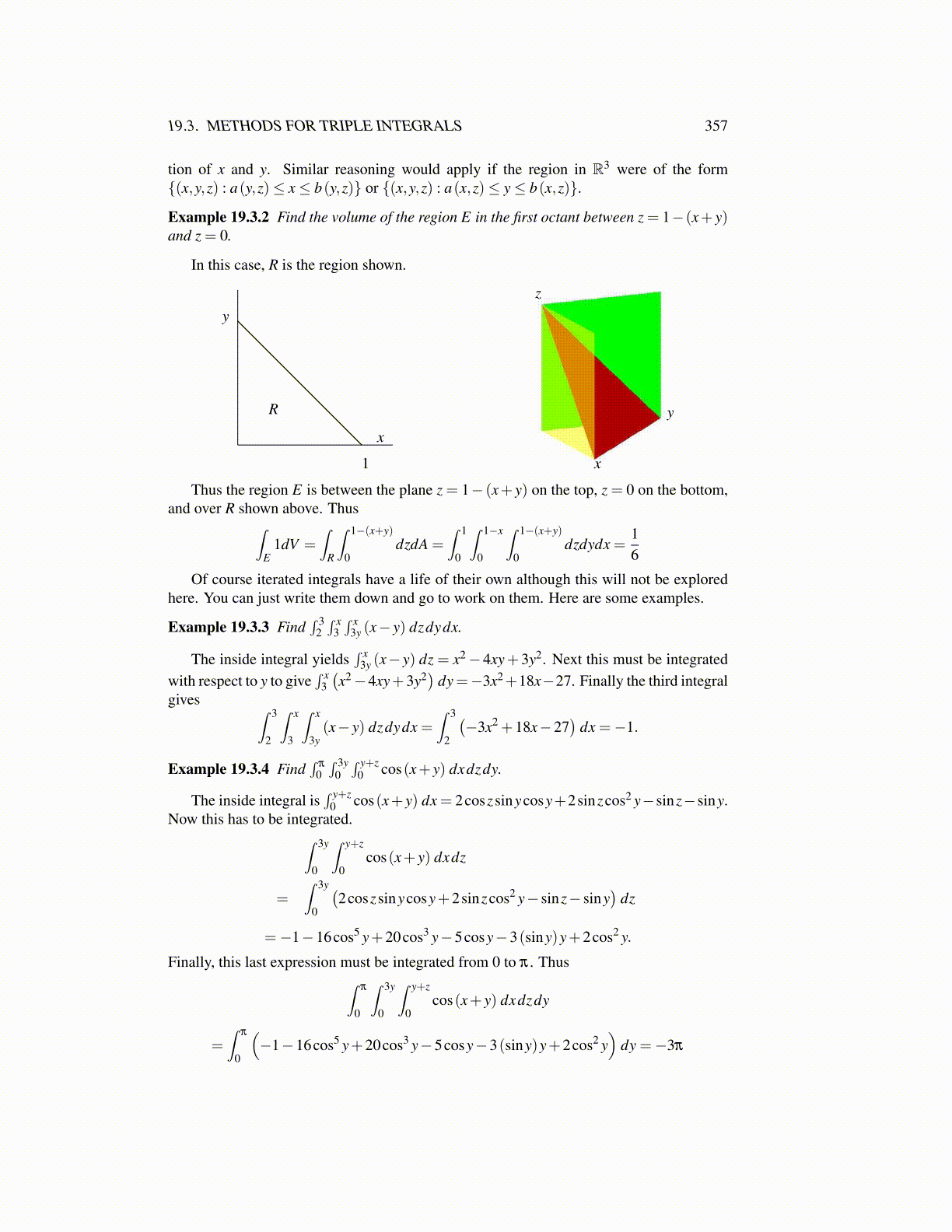
Example 19.3.2 Find the volume of the region E in the first octant between z = 1− (x+ y)and z = 0.
In this case, R is the region shown.
x
y
R
1 x
y
z
Thus the region E is between the plane z = 1− (x+ y) on the top, z = 0 on the bottom,and over R shown above. Thus∫
E1dV =
∫R
∫ 1−(x+y)
0dzdA =
∫ 1
0
∫ 1−x
0
∫ 1−(x+y)
0dzdydx =
16
Of course iterated integrals have a life of their own although this will not be exploredhere. You can just write them down and go to work on them. Here are some examples.
Example 19.3.3 Find∫ 3
2∫ x
3∫ x
3y (x− y) dzdydx.
The inside integral yields∫ x
3y (x− y) dz = x2−4xy+3y2. Next this must be integratedwith respect to y to give
∫ x3(x2−4xy+3y2
)dy=−3x2+18x−27. Finally the third integral
gives ∫ 3
2
∫ x
3
∫ x
3y(x− y) dzdydx =
∫ 3
2
(−3x2 +18x−27
)dx =−1.
Example 19.3.4 Find∫
π
0∫ 3y
0∫ y+z
0 cos(x+ y) dxdzdy.
The inside integral is∫ y+z
0 cos(x+ y) dx = 2coszsinycosy+2sinzcos2 y−sinz−siny.Now this has to be integrated.∫ 3y
0
∫ y+z
0cos(x+ y) dxdz
=∫ 3y
0
(2coszsinycosy+2sinzcos2 y− sinz− siny
)dz
=−1−16cos5 y+20cos3 y−5cosy−3(siny)y+2cos2 y.
Finally, this last expression must be integrated from 0 to π . Thus∫π
0
∫ 3y
0
∫ y+z
0cos(x+ y) dxdzdy
=∫
π
0
(−1−16cos5 y+20cos3 y−5cosy−3(siny)y+2cos2 y
)dy =−3π