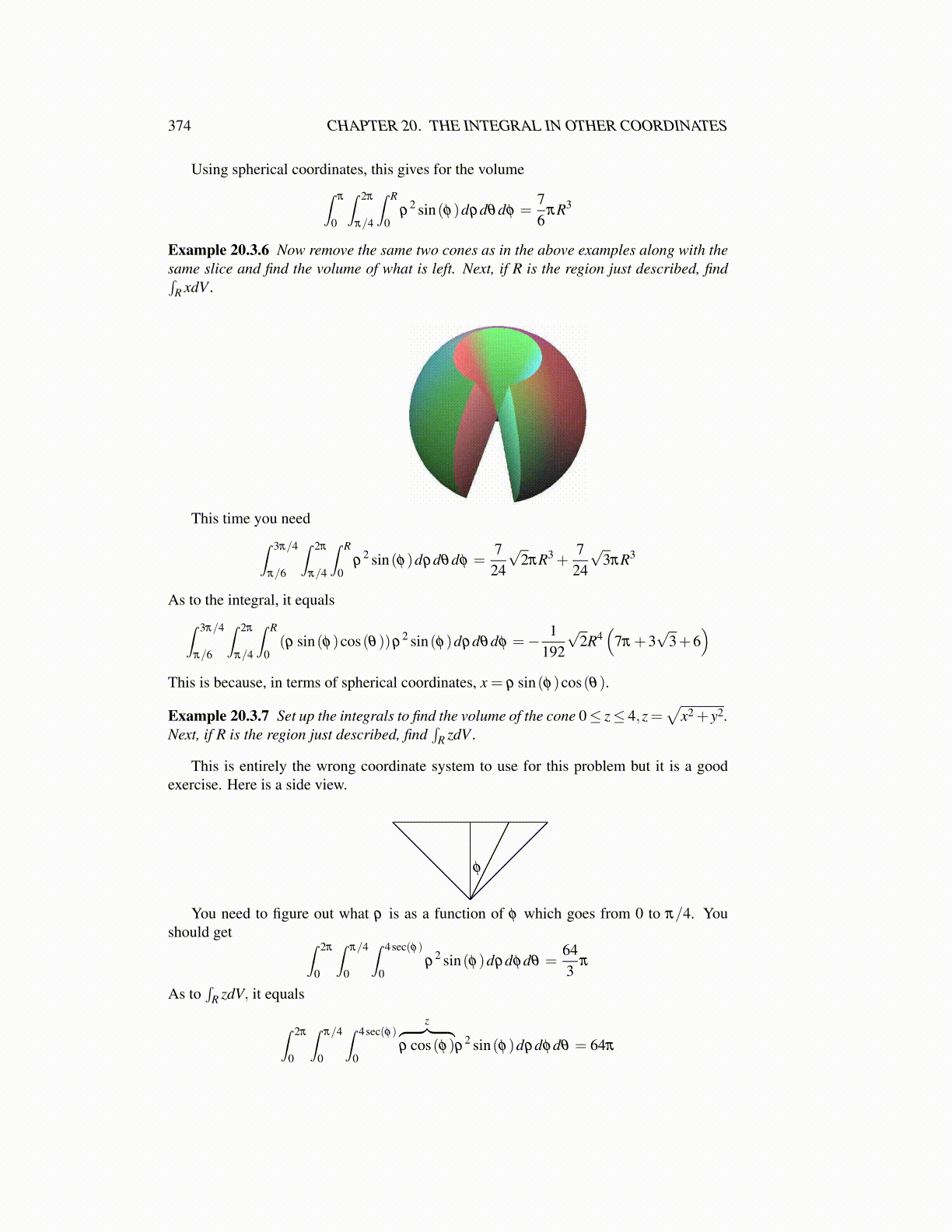
374 CHAPTER 20. THE INTEGRAL IN OTHER COORDINATES
Using spherical coordinates, this gives for the volume∫π
0
∫ 2π
π/4
∫ R
0ρ
2 sin(φ)dρdθdφ =76
πR3
Example 20.3.6 Now remove the same two cones as in the above examples along with thesame slice and find the volume of what is left. Next, if R is the region just described, find∫
R xdV .
This time you need∫ 3π/4
π/6
∫ 2π
π/4
∫ R
0ρ
2 sin(φ)dρdθdφ =7
24
√2πR3 +
724
√3πR3
As to the integral, it equals∫ 3π/4
π/6
∫ 2π
π/4
∫ R
0(ρ sin(φ)cos(θ))ρ
2 sin(φ)dρdθdφ =− 1192
√2R4
(7π +3
√3+6
)This is because, in terms of spherical coordinates, x = ρ sin(φ)cos(θ).
Example 20.3.7 Set up the integrals to find the volume of the cone 0≤ z≤ 4,z=√
x2 + y2.Next, if R is the region just described, find
∫R zdV .
This is entirely the wrong coordinate system to use for this problem but it is a goodexercise. Here is a side view.
φ
You need to figure out what ρ is as a function of φ which goes from 0 to π/4. Youshould get ∫ 2π
0
∫π/4
0
∫ 4sec(φ)
0ρ
2 sin(φ)dρdφdθ =643
π
As to∫
R zdV, it equals
∫ 2π
0
∫π/4
0
∫ 4sec(φ)
0
z︷ ︸︸ ︷ρ cos(φ)ρ2 sin(φ)dρdφdθ = 64π