14.1. THE POWER METHOD FOR EIGENVALUES 365
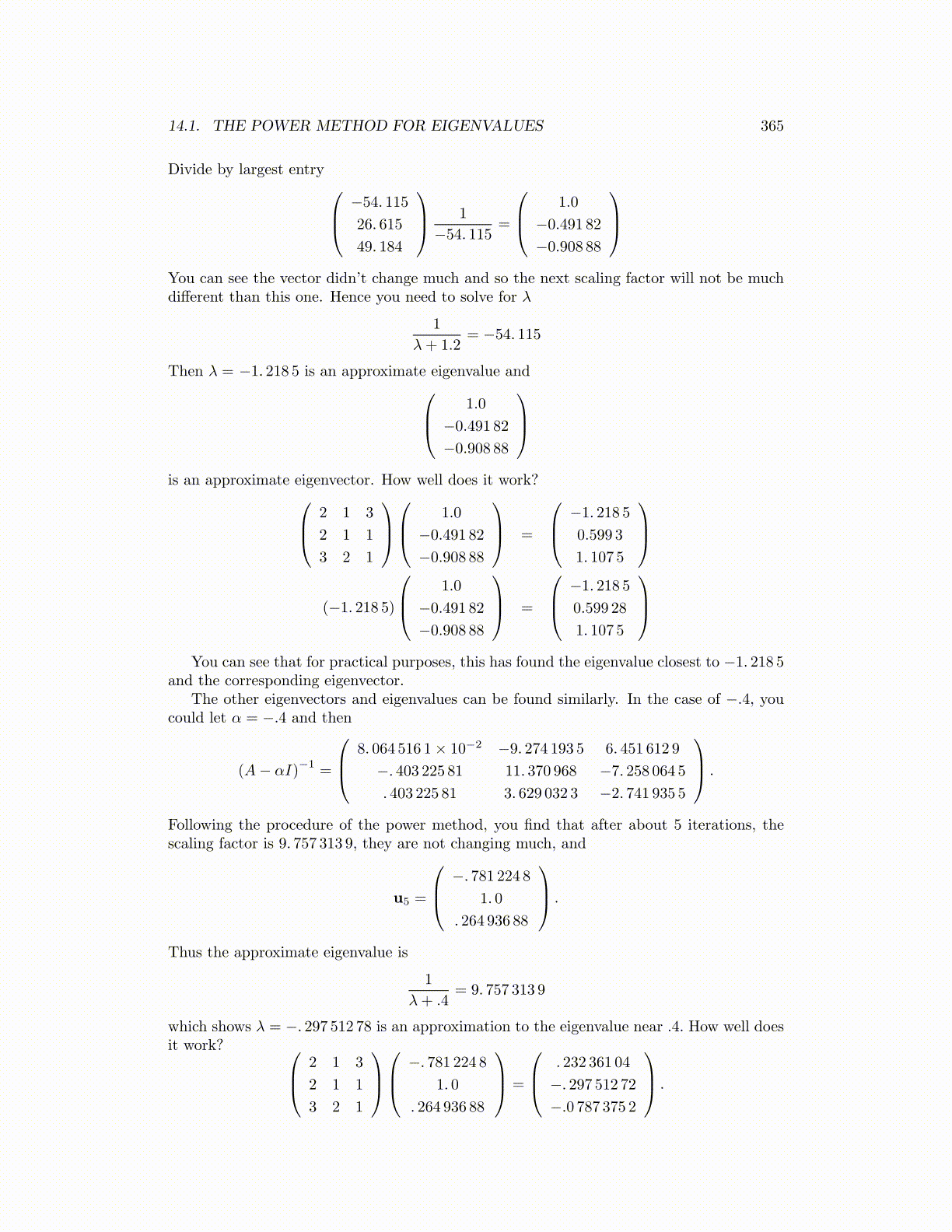
Divide by largest entry −54. 115
26. 615
49. 184
1
−54. 115=
1.0
−0.491 82
−0.908 88
You can see the vector didn’t change much and so the next scaling factor will not be muchdifferent than this one. Hence you need to solve for λ
1
λ+ 1.2= −54. 115
Then λ = −1. 218 5 is an approximate eigenvalue and 1.0
−0.491 82
−0.908 88
is an approximate eigenvector. How well does it work? 2 1 3
2 1 1
3 2 1
1.0
−0.491 82
−0.908 88
=
−1. 218 5
0.599 3
1. 107 5
(−1. 218 5)
1.0
−0.491 82
−0.908 88
=
−1. 218 5
0.599 28
1. 107 5
You can see that for practical purposes, this has found the eigenvalue closest to −1. 218 5
and the corresponding eigenvector.The other eigenvectors and eigenvalues can be found similarly. In the case of −.4, you
could let α = −.4 and then
(A− αI)−1
=
8. 064 516 1× 10−2 −9. 274 193 5 6. 451 612 9
−. 403 225 81 11. 370 968 −7. 258 064 5
. 403 225 81 3. 629 032 3 −2. 741 935 5
.
Following the procedure of the power method, you find that after about 5 iterations, thescaling factor is 9. 757 313 9, they are not changing much, and
u5 =
−. 781 224 81. 0
. 264 936 88
.
Thus the approximate eigenvalue is
1
λ+ .4= 9. 757 313 9
which shows λ = −. 297 512 78 is an approximation to the eigenvalue near .4. How well doesit work? 2 1 3
2 1 1
3 2 1
−. 781 224 8
1. 0
. 264 936 88
=
. 232 361 04
−. 297 512 72−.0 787 375 2
.